1. Einführung
„Fortnite“ ist derzeit in aller Munde und begeistert weltweit ein Millionenpublikum. In dem von Epic Games entwickelten Spiel kämpft man entweder alleine oder mit bis zu 3 Mitstreitern im Stile eines Battle Royales gegeneinander auf einer Insel. Dieses Genre bedienen nicht nur zahlreiche Games wie „Playerunkown's Battlegrounds“ oder „Totally Accurate Battlegrounds“, sondern auch Bücher und Filme wie „Die Tribute von Panem“.
Die Popularität von Fortnite zieht sich weltweit durch alle Gesellschaftsgruppen. Entrepreneur und Tesla-Chef Elon Musk teilte sogar einen Fake-Artikel über ihn mit seinen rund 23 Millionen Followern auf Twitter, in dem er angeblich Fortnite mit dem Ziel es zu löschen gekauft habe, um „die Jugend vor der ewigen Jungfräulichkeit“ zu bewahren.
Kurzum: Das Spiel erfährt aktuell einen großen Hype und bietet für viele eine Einstiegschance in den hart umkämpften Profizocker-Markt. Was liegt da also näher als nach Möglichkeiten zur Optimierung der eigenen Spielstrategie zu suchen? Und genau dabei soll Dir ausgerechnet der „Erzfeind Mathe“ helfen? Was für viele wie ein schlechter Scherz klingen mag, wird nach der Lektüre dieses Artikels gelebte Realität sein.
2. Die Problemstellung
Auf einer Karte der Insel kann der Spieler vor dem eigentlichen Kampf auswählen, wo er landen möchte. „Landen“ bedeutet in diesem Fall, dass man aus dem Luftschiff springt, sich für einige Zeit im freien Fall befindet und anschließend seinen Fallschirm öffnet, um die restlichen Meter zum Ziel zu gleiten. Je früher man festen Boden unter den Füßen hat, desto mehr Zeit verbleibt für das Sammeln von Waffen und dem Erkunden der Umgebung. Dabei gilt: Wer zuerst kommt, mahlt zuerst. Ein Teil des Optimierungsprozesses der eigenen Spielstrategie ist die Minimierung der „Landezeit“. Da mit der Simulation der realen physikalischen Gegebenheiten unserer Welt innerhalb eines Spiels immer eine Komplexitätsreduktion einhergeht, reichen bereits einfache mathematische Grundlagen aus, um eine erfolgsversprechende Strategie zu entwerfen und theoretisch nachzuweisen, dass sie tatsächlich funktioniert.
3. Ein früher Absprung lohnt sich!
Sobald sich der Spieler eine bestimmte Landeposition ausgesucht hat, heißt es im Normalfall zunächst warten, bis das Luftschiff über der entsprechenden Stelle thront. Dabei fliegt es mit konstanter Geschwindigkeit \(v_L\) und benötigt für das Zurücklegen der Strecke \(s\) vom Start bis zu Ziel eine bestimmte Zeit \(t_1\). Der funktionale Zusammenhang dieser drei Größen ist gegeben durch \(t_1=\frac{s}{v_L}\). Daran schließt für Gewöhnlich ein Sprung aus dem Luftschiff an, der direkt in eine Phase des freien Falls mündet. Der Spieler kann dabei selbst entscheiden, wie lange diese Phase dauert. Für die strategischen Überlegungen ist wichtig zu wissen, dass man im freien Fall wesentlich schneller ist als in der direkt anknüpfenden Phase des Gleitens. Die Formel zur Berechnung der Zeit direkt nach dem Absprung und vor dem Öffnen des Gleitschirms ist gegeben durch \(t_2=\sqrt{\frac{2\cdot h}{g}}\). Die Geschwindigkeit \(v_F\) lässt sich durch \(v_F=g\cdot t_2\) berechnen. Geht man davon aus, dass Fortnite auf der Erde spielt, ist \(g\approx 9.81 \frac{m}{s^2}\) (Erdbeschleunigung). \(h\) gibt die zurückgelegte Höhe zwischen dem Absprungpunkt und dem Öffnen des Gleitschirms an. Zum Schluss gleitet der Spieler (vereinfacht angenommen) mit der Geschwindigkeit \(v_G\) in Richtung des Gebäudes, wo er letztendlich landen möchte. Dafür benötigt er die Zeit \(t_3\). Die Gleitgeschwindigkeit ist allerdings geringer als im freien Fall</b></font> (\(v_G\lt v_F\)), was für das Zurücklegen derselben Höhe das Verhältnis \(t_3\gt t_2\) zur Folge hat. Es ist also sinnvoll, den Gleiterschirm so spät wie möglich zu öffnen. Der Nachteil einer längeren Wartezeit ist offensichtlich: Man kann sich nicht effektiv in Richtung des Gebäudes bewegen. Es muss also ein Kompromiss zwischen der Wahl von \(t_2\) und \(t_3\) gefunden werden. Insgesamt benötigt der Spieler die Zeit \(t=t_1+t_2+t_3\), bis er an seinem Zielort angekommen ist.
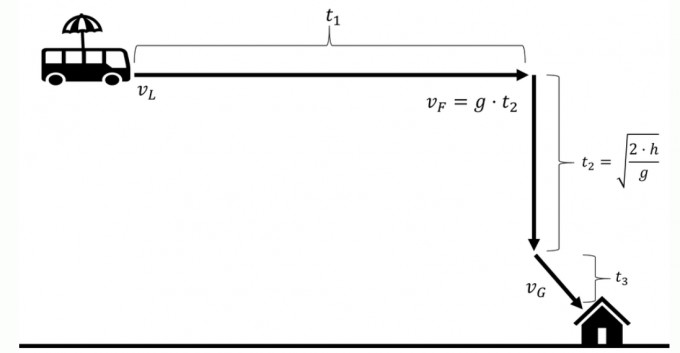
In der Regel ist \(t_1\) aufgrund der langsamen Geschwindigkeit \(v_L\) des Luftschiffs am längsten, d. h. \(t_2\lt t_3\lt t_1\). Je nach Lage des Luftschiffs und des Ziels kann es durchaus sinnvoll sein, direkt abzuspringen, sich kurzzeitig im freien Fall zu befinden und anschließend mit \(v_G\) in Richtung Gebäude zu gleiten. Dadurch nutzt man die sonst regungslos im Luftschiff verbrachte Zeit, um effektiv an Höhe zu verlieren und sich schneller dem Boden zu nähern. Auf diese Weise ergibt sich eine neue „Route“:
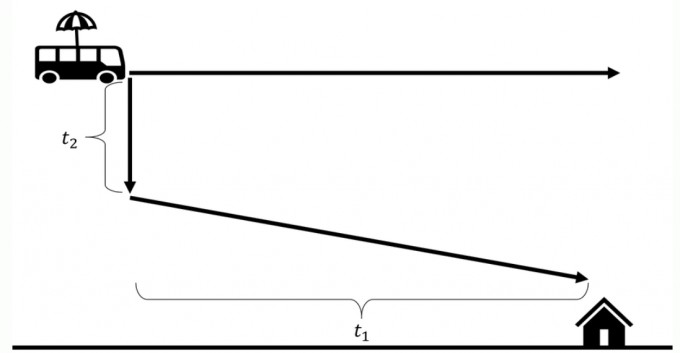
In dieser Konstellation benötigt man plötzlich nur noch \(t'=t_2+t_1\) Sekunden bis zum Ziel und spart dadurch \(t_3\) Sekunden ein. Der Erfolg lässt sich auch quantifizieren: Seien \(t_1=6s\) (\(6\) Sekunden im Luftschiff), \(t_2=4s\) (\(4\) Sekunden im freien Fall) und \(t_3=6s\) (\(6\) Sekunden gleiten). Mit der ersten Variante erreicht man das Gebäude nach \(t=6s+4s+6s=16s\), während man im zweiten Fall nur \(t'=6s+4s=10s\) braucht, was einem Boost von \(\frac{16s-10s}{16s}=\frac{4s}{16s}=37.5\%\) entspricht. Die Realität ist natürlich weitaus komplexer und es bedarf vieler praktischer ingame-Messungen. Für einen ersten sichtbaren Vorteil gegenüber den Gegnern reicht es aber allemal!
4. Erwäge den Lotabstand!
Befindet sich das Ziel nicht direkt auf der vorgegebenen Strecke, ist der ideale Absprungpunkt durch den Lotabstand gegeben:

Es ist erstaunlich, dass Begriffe wie „Normalenvektor“ auch das Zocker-Dasein bereichern können. Wer allerdings schon einmal ein Spiel programmiert oder eine VR-Landschaft modelliert hat, weiß das bereits. Für die Berechnung des optimalen Absprungpunkts reicht übrigens eine Abschätzung nach Augenmaß, da das Spielgeschehen selbstverständlich parallel weiterläuft und auch für den Mathematiker nicht auf wundersame Weise einfach pausiert.
Man sollte übrigens bedenken, dass es oft auch sinnvoll sein kann, nicht direkt abzuspringen. Vor allem dann nicht, wenn die Kontrahenten ebenfalls direkt das Schiff verlassen. Sobald die Spieler landen, beginnen nämlich bereits die gegenseitigen Kämpfe, was in Anbetracht geringer Ressourcen zu Beginn problematisch sein kann. Man sollte große Ansammlungen anfangs meiden, um erst einmal sein Inventar aufzufüllen.
5. Zusammenfassung
Statt zu warten, bis das (langsame) Luftschiff über das gewünschte Gebäude fliegt, ist es sinnvoll, so früh wie möglich abzuspringen, sich wenige Sekunden im freien Fall zu befinden und anschließend zu gleiten. Liegt das Ziel nicht auf der Luftschiffroute, kann man über den Lotabstand abschätzen, wo man abspringen muss, um einen möglichst geringen Weg zurücklegen zu müssen. Dabei sollten allerdings auch durch die Praxis erworbene Erfahrungswerte zur Abschätzung, ob eine lange Verweildauer im Luftschiff oder ein vorzeitiger Absprung schneller ist, genutzt werden.
Es handelt sich hierbei selbstverständlich um ein vereinfachtes Modell. Für eine detaillierte Analyse ist der Einblick in die Implementierung der Spielphysik, sowie eine ausführliche (praktische) Testreihe notwendig. Für erste Optimierungen sind diese Überlegungen allerdings vollkommen ausreichend und ermöglichen es Dir zukünftig einige Sekunden vor Deinen Mitstreitern auf der Insel zu landen.
Dieser Artikel hat 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.