Bernoulli - Stichprobe Flasche

Question

Aufgabe:

Der Hersteller garantiert ,dass 98 % der Flaschen mindestens 495 cm ^3 enthalten. Von der abgefüllten Flaschen wird eine Stichprobe von 20 Flaschen entnommen. Wie groß ist die Wahrscheinichkeit, dass mindestens zwei Flaschen weniger als 495cm^3 enthalten?

Answer 1

(1) Sei X die Anzahl unterbefüllter Flaschen in der Stichprobe, dann können wir X als binomialverteilt mit den Parametern n=20 und p=1-0.98=0.02 annehmen. Gesucht ist dann P(2≤X≤20).

(2) Sei alternativ zum oben Beschriebenen Y die Anzahl der Flaschen mit der garantierten Befüllung in der Stichprobe, dann können wir Y als binomialverteilt mit den Parametern n=20 und p=0.98 annehmen. Gesucht ist jetzt P(0≤X≤18).

(3) Es ist also erforderlich, die Daten aus der Aufgabe aufeinander abzustimmen. Ob dies so geschieht wie in (1), oder so wie in (2) ist im Prinzip egal. Manche Taschenrechner bieten allerdings nur die Variante (2) an. Meiner kann beides, hier die Ergebnisse:

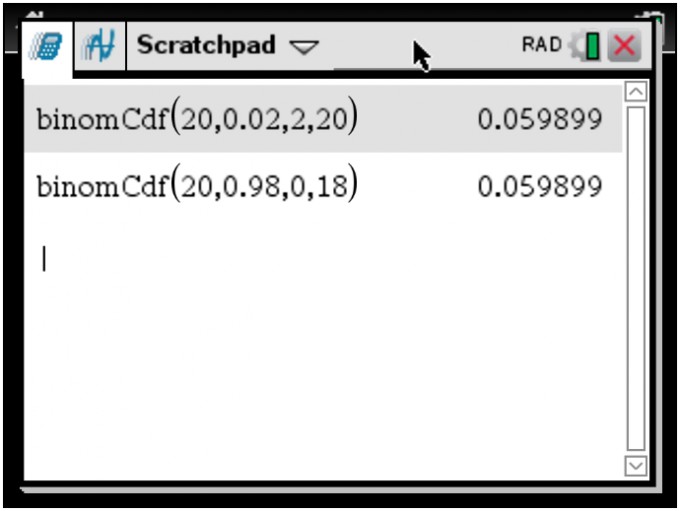
(4) Stehen keine Hilfsmittel mit kumulierter Binomialverteilung zur Verfügung, können die Varianten (1) und (2) auch mit Hilfe der Bernoulli-Formel berechnet werden. Dazu betrachtet man zweckmäßigerweise das jeweilige Gegenereignis. 

Comments

Erstmals vielen Dank für die ausführliche Antwort aber wie kommt man aus das Gegenereignis???

---

Erstmal vielen Dank für die ausführliche Antwort, aber wie kommt man auf das Gegenereignis?

Das ist nicht schwer. Im Falle von

(1) Sei X die Anzahl unterbefüllter Flaschen in der Stichprobe, dann können wir X als binomialverteilt mit den Parametern n=20 und p=1-0.98=0.02 annehmen. Gesucht ist dann P(2≤X≤20).

war das Ereignis, dass ich betrachtet hatte, 2≤X≤20. Dazu ist nun das Gegenereignis 0≤X≤1. Die gesuchte Wahrscheinlichkeit lässt sich damit dann so bestimmen:

P(2≤X≤20) = 1-P(0≤X≤1) = 1-P(X=0)-P(X=1)

Das lohnt sich aber nur dann, wenn man die hervorehobenen Wahrscheinlichkeiten mit der Bernoulli-Formel berechnen möchte und keine anderen Möglichkeiten benutzen will oder kann.

Answer 2

P(X>=2) = 1-P(X<=1) = 1-P(X=0)-P(X=1)

Mit der Gegenwahrscheinlichkeit gehts am schnellsten.

Comments

Wie kommt man aus das Gegenereignis???