Wahrscheinlichkeit berechnen, dass es sich um Marken-Rakete handelt

Question

Hey alle zusammen!

Ich wäre euch wirklich dankbar, wenn mir jemand nachrechnen könnte, ob ich hier richtig vorgegangen bin, bzw. oder der Rechenweg stimmt... habe leider schon eine Weile keine Warhscheinlichkeitrechnungen mehr gemacht...

Aufgabe:

Bei einer Silversterparty werden aufgrund eines akuten Budgetmangels nur 67% der Raketen von einem renommierten Markenhersteller bezogen, die restlichen sind billige No-Name-Raketen. 3% der Marken-Raketen und 20% der No-Name-Raketen sind "Blindgänger", dh. die Raketen können trotz Abbrennen der Zündschnur nicht abgefeuert werden.

Als die letzte Rakete gezündet wird, beginnt diese fürchterlich nach Schwefel zu stinken und kann nicht abgefeuert werden. Mit welcher Wahrscheinlichkeit handelt es sich dabei um eine der teuren Marken-Raketen?

Hier mein Lösungsweg:

!

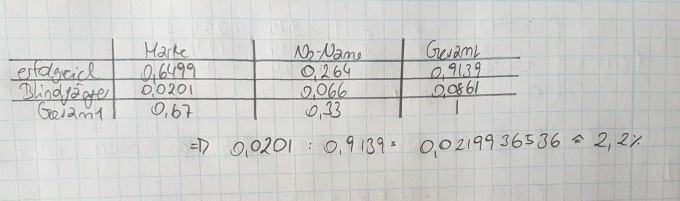
Comments

siehe auch
https://www.mathelounge.de/453547/welcher-wahrscheinlichkeit-handelte-dabei-marken-rakete

---

Vielen, vielen Dank euch allen für die schnellen, hilfreichen Rückmeldungen, und dafür, dafür dass ihr mich auf den Denkfehler hingewiesen habt!

Answer 1

Mit der Wahrscheinlichkeit

    67%·3% / (67%·3% + (100%-67%)·20%)

handelt es sich dabei um eine der teuren Marken-Raketen

Answer 2

P(Marke|Blindgänger) = P(Marke∩Blindgänger)/P(Blindgänger)=0,0201/0,0861≈23,34%

Answer 3

Deine Vierfeldertafel ist richtig und du bist beim berechnen nur beim Ablesen in die falsche Zeile gerutscht.