regelmäßige Sechsecke haben die angenehme Eigenschaft, dass der Radius \(r\) ihres Umkreises identisch mit der Seitenlänge \(a\) ist. Man kann so ein Sechseck in sechs gleichseitige Dreiecke zerlegen.
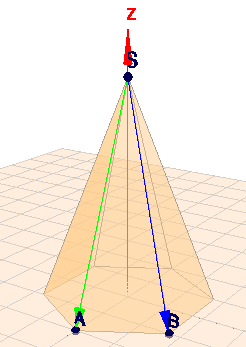
Gesucht ist der Winkel zwischen dem grünen und blauen Vektor, die beide vom Punkt \(S\) ausgehen. Wenn Du die Vektoren aufstellst so erhältst Du (wg. der gleichseitigen Dreiecken (s.o.))$$\vec{SA} = \begin{pmatrix} -a\\ 0 \\ -h\end{pmatrix}, \quad \vec{SB} \begin{pmatrix} -\frac 12 a\\ \frac 12 \sqrt 3 \, a \\ -h\end{pmatrix} $$ \(h\) ist hier die Höhe der Pyramide. Das ist übrigens identisch mit dem, was in Rolands Antwort steht (s. dort). Den Winkel \(\varphi\) zwischen zwei Winkeln kann man berechnen aus$$\begin{aligned} \cos \varphi &= \frac{\vec{SA} \cdot \vec{SB}}{|\vec{SA}|\cdot |\vec{SB}|} = \frac{\frac 12 a^2 +h^2}{h^2 + a^2} \\ & = \frac{\left( \frac ha \right)^2 + \frac 12}{\left( \frac ha \right)^2 +1}\end{aligned}$$D.h. Der Cosinus des Winkel - also auch der Winkel selbst - ist eine Funktion des Verhältnisses Höhe \(h\) zu Seite \(a\).
(PS.: klick auf das Bild, dann siehst Du es in 3D)
Weil Sommerferien sind und nicht so viele Fragen hatte ich noch Zeit für ein Goody:
https://jsfiddle.net/rLqgsd97/
Es ist eine geometrische Konstruktion des gesuchten Winkels \(\varphi\). Wenn $$\frac ha = \tan x$$ ist, so kann man das umformen in $$\cos \varphi = \frac{\tan^2 x + \frac 12}{\tan^2 x + 1} = \frac 14 \left( 3-\cos\left( 2x\right)\right)$$Darauf beruht obige Konstruktion. Der Punkt \(S\) ist die Spitze der Pyramide. \(|AM|\) ist der Radius bzw. eine Seite der Grundfläche.
Verschiebe den Punkt \(S\) und Du kannst sehen wie sich der Winkel \(\varphi\) zwischen der blauen und roten Geraden verändert.
Gruß Werner