Winkelberechnung zwischen Seitenkanten bei gleichmäßiger sechseckiger Pyramide

Question

Aufgabe:

wie ändert sich der Winkel der Seitenkanten einer gleichmäßigen sechseckigen Pyramide im Verhälnis zu deren Höhe-- oder wie berechnet man den Winkei der Seitenkanten bei sechseckiger gleichmäßiger Pyramide in Abhängigkeit ihrer Höhe

Comments

wie berechnet man den Winkei der Seitenkanten bei sechseckiger gleichmäßiger Pyramide in Abhängigkeit ihrer Höhe

Es gibt eine zweite Abhängigkeit. Welche soll das sein?

---

Die zweite Abhängigkeit ist natürlich der Radius des innen Kreises oder des aussen kreises der 6eckigen Grundfäche. Die Grundfläche soll erst mal als konstant betrachtet werden -- nür die Höhe ändert sich und somit der Winkei der Seitenlinen der Seitenflächen  --- aber wie

---

Die zweite Abhängigkeit ist natürlich der Radius des innen Kreises oder des aussen kreises der 6eckigen Grundfäche.

Du musst dich schon entscheiden, welche von diesen beiden Möglichkeiten du als zweite Abhängigkeit verwenden möchtest. Als dritte, vierte und fünfte Möglichkeiten stünden noch die Seitenlänge des Sechsecks, das Volumen der Pyramide und die Oberfläche der Pyramide zur Verfügung. Und es gibt nöch etliche weitere. Keine dieser Möglichkeiten ist natürlicher als irgend eine andere.

Answer 1

regelmäßige Sechsecke haben die angenehme Eigenschaft, dass der Radius $r$ ihres Umkreises identisch mit der Seitenlänge $a$ ist. Man kann so ein Sechseck in sechs gleichseitige Dreiecke zerlegen.

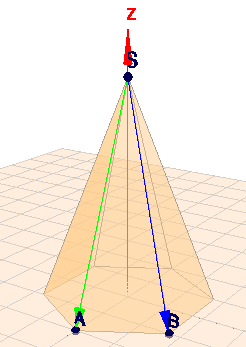
Gesucht ist der Winkel zwischen dem grünen und blauen Vektor, die beide vom Punkt $S$ ausgehen. Wenn Du die Vektoren aufstellst so erhältst Du (wg. der gleichseitigen Dreiecken (s.o.))$$\vec{SA} = \begin{pmatrix} -a\\ 0 \\ -h\end{pmatrix}, \quad \vec{SB} \begin{pmatrix} -\frac 12 a\\ \frac 12 \sqrt 3 \, a \\ -h\end{pmatrix}$$ $h$ ist hier die Höhe der Pyramide. Das ist übrigens identisch mit dem, was in Rolands Antwort steht (s. dort). Den Winkel $\varphi$ zwischen zwei Winkeln kann man berechnen aus$$\begin{aligned} \cos \varphi &= \frac{\vec{SA} \cdot \vec{SB}}{|\vec{SA}|\cdot |\vec{SB}|} = \frac{\frac 12 a^2 +h^2}{h^2 + a^2} \\ & = \frac{\left( \frac ha \right)^2 + \frac 12}{\left( \frac ha \right)^2 +1}\end{aligned}$$D.h. Der Cosinus des Winkel - also auch der Winkel selbst - ist eine Funktion des Verhältnisses Höhe $h$ zu Seite $a$.

(PS.: klick auf das Bild, dann siehst Du es in 3D)

Weil Sommerferien sind und nicht so viele Fragen hatte ich noch Zeit für ein Goody:

https://jsfiddle.net/rLqgsd97/

Es ist eine geometrische Konstruktion des gesuchten Winkels $\varphi$. Wenn $$\frac ha = \tan x$$ ist, so kann man das umformen in $$\cos \varphi = \frac{\tan^2 x + \frac 12}{\tan^2 x + 1} = \frac 14 \left( 3-\cos\left( 2x\right)\right)$$Darauf beruht obige Konstruktion. Der Punkt $S$ ist die Spitze der Pyramide. $|AM|$ ist der Radius bzw. eine Seite der Grundfläche.

Verschiebe den Punkt $S$ und Du kannst sehen wie sich der Winkel $\varphi$ zwischen der blauen und roten Geraden verändert.

Gruß Werner

Comments

Hallo Werner,

danke für die Antwort--aber das ist nicht der Winkel den ich meine ! ich meine den Winkel , den die Seitenlinien zueinander haben von S aus gesehen. Den Winkel jeder der 6 Seitenflächen, der gegegenüber der Grundkante des Sechecks. Dieser Winkel ändert sich doch auch mit der Länge von M - S .

---

Hallo Rolf,

aber das ist nicht der Winkel den ich meine

... habe ich inzwischen auch bemerkt :-/ und meine Antwort überarbeitet.

---

Hallo Werner ,

ist Super Danke----

So einen Mathelehrer hätt ich damals ( ist schon ne ganze ganze Weile her ) wohl gebraucht.-- Ich habs jetzt sogar verstanden -- das von Roland war ---- hm ---da war doch mal was --soo lange her -----aber was----------??-Du hast echt genial dargestellt-----Bin begeistert nochmal vielen Dank.

Grüßle aus dem Schwabenland

Rolf

---

.. das freut mich, dass ich Dir helfen konnte :-)

---

Nochmal danke !!!!

Answer 2

Lege die Grundfläche der Pyramide in die xy-Ebene und die Höhe h auf die z-Achse. Dann ist die vektorielle Darstellung zweier nebeneinandeliegender Seitenkanten $\begin{pmatrix} cos(0)\\sin(0)\\-h \end{pmatrix}$ und $\begin{pmatrix} cos(π/3)\\sin(π/3)\\-h \end{pmatrix}$. Für den Winkel zwischen zwei Vektoren gibt es eine Formel.