Aufgabe:
Eine Gruppe von Hochseilartisten spannt ein Stahlseil zwischen 2 senkrechten Masten, die 400m voneinander entfernt sind. Der Verlauf des Stahlseils wird beschrieben durch die Funktion
f(x)=5*(e^(0,01x)+e^(-0,01x))
A) Welche Höhe hat das seil in der Mitte bzw. In den randpunkten
B) Welche durchschnittliche Steigung bewältigt ein Artist bei der Fahrt von der Mitte des seils zu einem der Randpunkte?
C) ein Artist soll Steigungen bis maximal 20% bewältigen. Kann er die mittlere Hälfte des Seilshaften befahren?
Problem/Ansatz:
Ich habe leider keinen 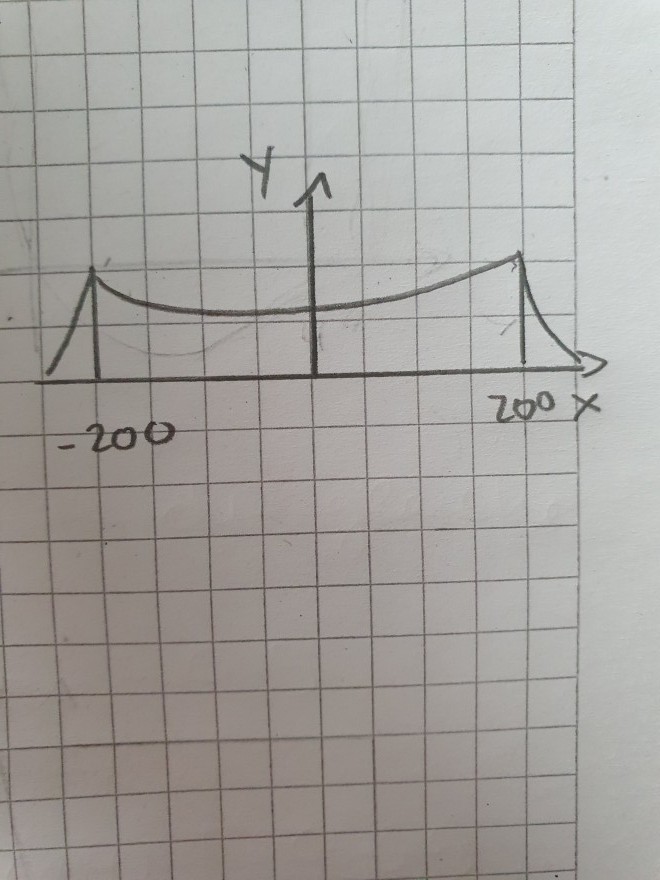
Text erkannt:
\( \frac{1}{1} \)