Hallo Izet,
Auch graphisch!
Um es graphisch zu lösen, betrachte ein Koordinatensystem, wo Rechtecke so eingezeichnet werden, dass zwei Seiten mit den Koordinatenachsen zusammen fallen und folglich eine Ecke stets im Koordinatenursprung liegt.
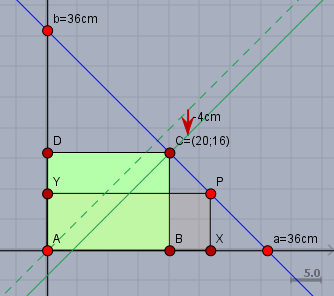
Der obere rechte Eckpunkt aller Rechtecke, die einen Umfang von 72cm haben, liegt dann auf der oben eingezeichneten blauen Geraden. Wählst Du dort einen Punkt \(P\) und vervollständigst das Rechteck durch die Punkte \(X\) und \(Y\), so hat das Rechteck \(AXPY\) einen Umfang von 72cm. Und es ist egal, wo auf der blauen Geraden \(P\) gewählt wird.
Die oberen rechten Eckpunkte aller Quadrate liegen auf der Winkelhalbierenden des 1.Quadranten - die grün gestrichelte Gerade. Und alle Rechtecke, bei denen die vertikale Seite um 4cm kürzer ist, als die waagerechte liegen demnach auf einer Geraden die 4cm unterhalb der Geraden der Quadrate liegt. Das ist die grüne durchgezogenen Gerade.
Die Lösung der Aufgabe ist also der Schnittpunkt \(C\) der blauen und der grünen Gerade. Und der liegt bei \(C=(20;16)\) mit dem Rechteck \(ABCD\).