extremale Werte über Einheitsbogen

Question

Hallo. Ich habe diese Aufgabe: Finde extremale Werte über dem Einheitsbogen von f:R^2->R, (x,y)->2x(y-0,5)

Ich habs analog zu meinem Mathekurs gemacht:

wegen dem Einheitsbogen erhalte ich: g: R^2->R, (x,y)->x²+y²-1
grad f(x,y)=(2y-1,2x)

grad f(x,y)=λ*grad g(x,y)

dann bekomme ich drei gleichungen:

y=λx+0,5

x=λy

x²+y²=1

x und y eingesetzt in die dritte gleichung ergibt:
λ²+λx-0,75=0

 pq-formel:
λ=-(x/2)±√((x²/4)+0,75)

das ist alles um die kritischen Punkte zu finden aber ab hier kriege ich nurnoch Quatsch raus, kann mir jemand heflen?

Comments

Sollt ihr das mit Lagrange machen? Dann verwirrt mich deine Schreibweise etwas.

---

mein prof hat noch nichts von lagrange erzählt also glaube ich nicht dass das so heißt. er sagte aber was von nebenbedingungen

---

Was du hier versuchst, ist das Lagrange verfahren.

https://de.m.wikipedia.org/wiki/Lagrange-Multiplikator

Wenn du λ berechnest, dürften x und y in der letzten Gleichung nicht mehr auftreten.

---

okay danke werde es versuchen

---

Du hast es schon fast richtig, siehe die Antwort von Mathecoach.

Answer 1

L(x, y, λ) = 2·x·(y - 0.5) - λ·(x^2 + y^2 - 1)

L'x(x, y, λ) = - 2·λ·x + 2·y - 1 = 0 --> y = λ·x + 0.5

L'y(x, y, λ) = 2·x - 2·λ·y = 0 --> x = λ·y

x^2 + y^2 - 1 = 0

Also mit Lagrange sieht das alles so aus wie bei dir ...

Günstiger ist es aber bei den ersten beiden Gleichungen das Lamda zu eliminieren

- 2·λ·x + 2·y - 1 --> λ = (2·y - 1)/(2·x)

2·x - 2·λ·y = 0 --> λ = x/y

(2·y - 1)/(2·x) = x/y → x^2 = y^2 - 0.5·y

(y^2 - 0.5·y) + y^2 - 1 = 0 --> y = -0.5930703308 ∨ y = 0.8430703308

Achtung das ist jetzt nur die Lösung für y.

Vergleichslösung über Wolfram

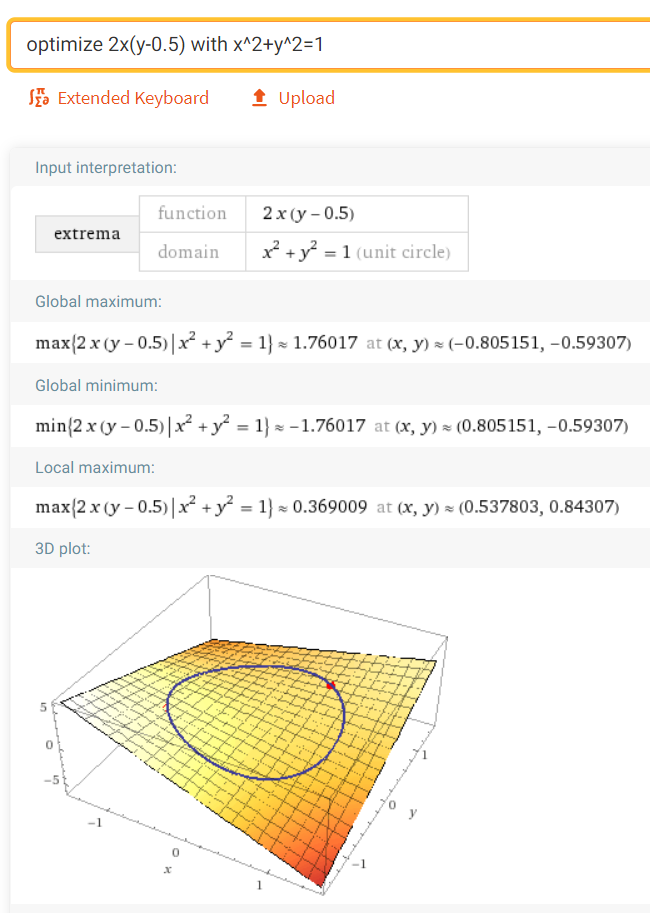
Huch. Fehlt hier bei Wolframalpha etwa ein lokales Minimum?

Das solltest du auf jeden Fall nochmal prüfen.

Aber Wolframalpha bestätigt den Wert für y. Also kannst du genau dort weitermachen.

Comments

ok bis dahin kann ich es total nachvollziehen aber wie mache ich das für x? ich hab für y^2=x^2-0,5y was mir ja garnix bringt :/

---

Do. Dort setzt du x ein und kannst nach y Auflösen. Das ist auch eine normale quadratische Gleichung die du über pq-Formel lösen kannst.

---

verstehe ich nich...

habe y²=x²+0,5

und da x² einsetzen meinst du? oder x= λ*y?

wenn ich x² einsetze bekomme ich y=1

---

Sorry. meinte y einsetzen.

y = 0.8430703308

x^2 = y^2 - 0.5·y

x^2 = 0.8430703308^2 - 0.5·0.8430703308 --> x = ±0.5378033258

Genau so für das andere y.

---

vielen dank dass du immer so schnell antwortest und hilfst lieber Mathecoach :-)

ich habe jetzt y1,y2 und x1,x2,x3,x4

jetzt muss ich vermutlich nurnoch prüfen für welche x-y- variationen der grad =0 wird, korrekt?

wobei da kommt man nie exakt auf 0 merke ich grade ^^

---

also ich glaube (x,y) x und y beide + und beide - bedeutet maximum. und eins + eins - bedeutet minimum. aber dann komme ich auf sehr viele extreme punkte dabei soll ich doch nur 4 haben? ich schätze dass ich eigentlich nur zwei x haben darf  und nicht vier

---

die vierte minima stelle müsste bei (-0,53780/0,84307) nach der Abbildung in Wolfram Alpha sein. aber wie komme ich ohne Wolfram Alpha auf die Extremstellen?

---

die vierte minima stelle müsste bei (-0,53780/0,84307) nach der Abbildung in Wolfram Alpha sein. aber wie komme ich ohne Wolfram Alpha auf die Extremstellen?

Die hab ich doch schon oben ausgerechnet

x^2 = 0.84307033082 - 0.5·0.8430703308 → x = ±0.5378033258

Also sind zwei mögliche Extremstellen

(-0.5378 | 0.8431) und (0.5378 | 0.8431)

dort wird der grad auch näherungsweise null. er würde exakt null sein wenn du nicht mit gerundeten werten gerechnet hättest.

Wenn du dann noch die Funktionswerte berechnest ist klar das es zwei hoch und zwei Tiefpunkte sind.

---

ja ich meinte aber mit der passenden y stelle. nagut danke

---

Wieso passt die y Stelle nicht? Das sind die doch aus Wolframalpha.

---

du hast mich eben nicht ganz verstanden, aber ich hab es jetzt fertig alles gut :-)