Wie kann man auf einfachste Weise äussere Tangenten zweier Kreise berechnen?

Question

Aufgabe:

Wie kann man äussere Tangenten zweier Kreise berechnen?

Problem/Ansatz:

Tangenten müssen immer im richtigen Winkel sein, egal wie die Kreise liegen.

Comments

Hallo Anna,

bist Du bereits mit den Grundlagen der Vektorrechnung vertraut?`

Wäre es für Dich verständlich, wenn $m$ (ein Vektor) der Mittelpunkt des Kreises ist, $r$ (eine Zahl) der Radius und $(x-m)^2 = r^2$ die Gleichung für alle Punkte $x$ ist, die auf dem Kreis liegen? Evt. schreibst Du das auch so: $(\vec x - \vec m)^2=r^2$

Answer 1

Hallo Anna,

Angenommen, die Mittelpunkte der beiden Kreise sind $m_1$ und $m_2$ und die zugehörigen Radien $r_1$ und $r_2$, wobei $r_2 \ge r_1$ . Das Ziel ist es, zunächst ein Paar Einheitsvektoren $n_{a,b}$ (rot) zu berechen, die vom Mittelpunkt der Kreise zu den Berührpunkten $q_{1,2}$ der Tangente $t_a$ und den Berührpunkten $q_{1,2}'$ der Tangente $t_b$ (braun) zeigen. Es gilt $$q_{1,2} = m_{1,2} + r_{1,2} \cdot n_a, \quad q_{1,2}' = m_{1,2} + r_{1,2} \cdot n_b, \quad |n_{a,b}|=1$$

 

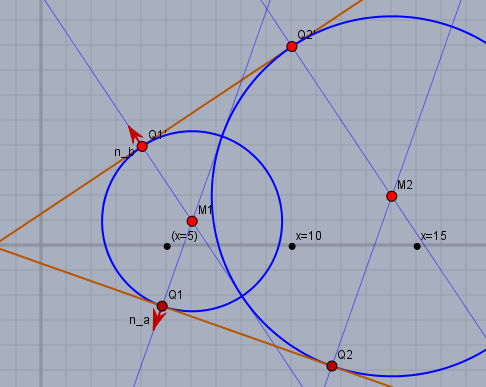
Berechne dazu die Vektoren $d$ und $d^\perp$, sowie den Wert $e$ wie folgt:$$\begin{aligned} d &= \frac{m_1-m_2}{|m_1-m_2|}, \quad e = \frac{r_2-r_1}{|m_1-m_2|} \end{aligned}$$jetzt sollte $e\ge 0$ sein. Falls nicht, so multipliziere bitte $d$ und $e$ mit $-1$. Dann ist noch $d^\perp$:$$d ^\perp = \begin{pmatrix} -d_y\\d_x \end{pmatrix}$$Daraus lassen sich die beiden Normalenvektoren $n_{a,b}$ berechnen:$$n_{a,b} = ed \pm \sqrt{1-e^2}\, d^\perp$$und damit kannst Du nun einfach z.B. $q_1$ berechnen:$$q_1 = m_1 + r_1 \cdot n_a$$und die zugehörige Tangente $t_a$ ist dann$$\begin{array}{lll} t_a: &n_a \cdot x &= n_a \cdot q_1 \\ t_a: &x &= q_1 + \lambda \cdot n_a^\perp, \quad n_a^\perp = \begin{pmatrix} -n_{ay}\\n_{ax} \end{pmatrix} \end{array}$$einmal in Normal- und einmal in Punkt-Richtungsform.

In obigen Bild ist (rechne es ruhig mal nach)$$m_1= \begin{pmatrix}6\\ 1\end{pmatrix}, \quad r_1 = \sqrt{13} \\ m_2 = \begin{pmatrix}14\\ 2\end{pmatrix}, \quad r_2 = 2\sqrt{13} \\ d = \frac 1{\sqrt{65}} \begin{pmatrix}-8\\ -1\end{pmatrix} , \quad e = \frac{1}{\sqrt 5} \\ n_a = \frac{1}{5 \sqrt{13}} \begin{pmatrix}-6\\ -17\end{pmatrix}, \quad n_b = \frac 1{\sqrt{13}}\begin{pmatrix}-2\\ 3\end{pmatrix} \\ q_1 = \begin{pmatrix}4.8\\ -2.4\end{pmatrix}, \quad q_1' = \begin{pmatrix}4\\ 4\end{pmatrix}$$

Falls Du mehr darüber wissen möchtest oder Fragen hast, so melde Dich bitte.

Nachtrag: alles zusammen gefasst lautet die Formel für die Vektoren $n_{a,b}$ $$\begin{aligned} \Delta m &= m_1 - m_2, \quad \Delta m^\perp = \begin{pmatrix} -\Delta m_y\\ \Delta m_x \end{pmatrix} \\ \Delta r &= r_2-r_1 \\ n_{a,b} &= \frac {\Delta r\Delta m\pm \sqrt{(\Delta m)^2 - (\Delta r)^2} (\Delta m)^\perp}{(\Delta m)^2} \\ &= \frac 1{(\Delta m)^2} \begin{pmatrix} \Delta m & (\Delta m)^\perp \end{pmatrix} \begin{pmatrix} \Delta r\\ \pm \sqrt{(\Delta m)^2 - (\Delta r)^2} \end{pmatrix} \end{aligned}$$Die letzte Zeile zeigt die Formel in Matrixschreibweise, was praktisch ist, wenn man z.B. ein Tabellenkalkulationsprogramm benutzt oder in einem Programm.

Comments

Könntest Du mir verraten, was für eine Formatierung das ist, die Du nutzt?

Kann es so schlecht entziffern.

##hat sich erledigt##wird jetzt normal angezeigt##

---

Könntest Du mir verraten, was für eine Formatierung das ist, die Du nutzt?

Das ist die Standardformatierung hier plus die LaTeX-Funktion - siehe auch den LaTeX-Assistenten.

Kann es so schlecht entziffern.

Oh!? - was siehst Du denn? LaTeX liefert normalerweise ein sehr gutes Schriftbild - oder siehst Du nur den 'Source-Code'? Was für einen Browser benutzt Du?

Was siehst Du hier?: $$\int_a^b x^2\, \text dx + \sum_{k=0}^n k^2$$Sehen solltest Du dies:

Chrome oder Firefox sollten problemlos alles anzeigen

---

Was passiert, wenn r1<r2?

Spielt es eine Rolle?

---

Was passiert, wenn r1<r2?

Ich ahne, dass Du was programmierst ... ;-)

Wenn $r_1 \lt r_2$ ist, wird der Wert von $e$ negativ. Deshalb habe ich oben in meiner Antwort bereits geschrieben, dass dann die Gleichung, bzw, die Werte von $e$ und $d$ mit $-1$ zu multiplizieren sind. Was aber wiederum unnötig ist, da sich das in der Folgerechnung wieder aufhebt.

Wenn Du es programmierst, so nutze besser die geschlossene Form für die Vektoren $n_{a,b}$. Ich habe das noch an meine Antwort angehängt (s.o.).

Wichtig ist nur, dass Du $\Delta r$ und $\Delta m$ richtig rechnest (s.o.); einmal steht der Index 1 vorn und einmal der Index 2. Dann spielen die Größenverhältnisse von $r_{1,2}$ keine Rolle mehr.

Welche Programmiersprache?

---

Javascript.

=1−2|1−2|

diese Formel berechne ich so:

dx = m1x-m2x/ Abstand:m1m2

dy = m1y-m2y/ Abstand:m1m2

Passt das?

---

Passt das?

Ja, wenn das '/' einen Kommentar einleitet und der Rest der Zeile ignoriert wird. Ansonsten empfehle ich bei sowas eine eigene Klasse zu verwenden, die einen (mathematischen) Vektor implementiert. Weiß aber nicht, ab Javascript das kann.

---

Also Punkt q1 ist korrekt.

Leider kann ich die Tangente nicht berechnen, weil ich nicht weiß was λ ist.

---

Leider kann ich die Tangente nicht berechnen, weil ich nicht weiß was λ ist.

für jeden Wert λ ergibt sich genau ein Punkt der Tangente. Da man unendlich viele Werte für λ einsetzen kann hat man hier eine Gerade die aus unendlich vielen Punkten besteht.

---

Irgendwie passt es nicht. Die Punkte sind zwar auf den Kreisen, aber die Tangenten sind keine Tangenten.

---

let distance =(Math.sqrt(Math.pow(arrayCircle.x()-minCircle.x(), 2) + Math.pow(arrayCircle.y()-minCircle.y(), 2)));
l

Das ist die Berechnung. Passt leider nicht. Die Linien schneiden die Kreise.

//Abstand m1m2

let dx = (arrayCircle.x()-minCircle.x())/distance;
let dy = (arrayCircle.y()-minCircle.y())/distance;

let dTangentx= -dy;
let dTangenty=dx;
//e berechnen
let e = (arrayCircle.radius()-minCircle.radius())/distance;
//Normalvektoren berechnen
let naX = e*dx+Math.sqrt(1-Math.pow(e,2))*dTangentx;
let naY = e*dy+Math.sqrt(1-Math.pow(e,2))*dTangenty;
let nbX = e*dx-Math.sqrt(1-Math.pow(e,2))*dTangentx;
let nbY = e*dy-Math.sqrt(1-Math.pow(e,2))*dTangenty;
//Berührpunkte berechnen
let qx1 = arrayCircle.x()+(arrayCircle.radius()*naX);
let qy1 = arrayCircle.y()+(arrayCircle.radius()*naY);
let qx2 = minCircle.x()+(minCircle.radius()*naX);
let qy2 = minCircle.y()+(minCircle.radius()*naY);

//Punkte der Tangente
let tangentPoints =[qx1,qy1,qx2,qy2];

---

es ist kein offensichtlicher Fehler zu sehen. Wo laufen die 'Tangenten'? Vielleicht durch den Mittelpunkt oder vielleicht so:

?

PS.: ich fände es gut, wenn Du mehr Feedback gibst.

---

Leider Vom Berührpunkt aus schneiden sie einen Kreis und gehen zum nächsten Berührpunkt.

---

Leider Vom Berührpunkt aus schneiden sie einen Kreis und gehen zum nächsten Berührpunkt.

nach dieser Beschreibung sind entweder drei Kreise pro Tangente involviert oder die Tangenten sind keine Geraden ??

---

Zeige bitte mal den Code, der das $\Delta r$ berechnet.

---

Die roten Tangenten sind die, die gezeichnet werden. Die blauen, wie sie sein sollten.

---

let e = (arrayCircle.radius()-minCircle.radius())/distance;

hier ist der Fehler. Ich glaub' ich habe es inzwischen dreimal geschrieben!! Es muss heißen:

let e = (minCircle.radius()-arrayCircle.radius())/distance;

---

STIMMT!!!!!!DANKE!!!!!!!

---

Der Vektor d, ist der Verbindungsvektor zwischen M1 und M2 ?

Der Vektor n ist ein Normalenvektor, das heißt dieser Vektor ist orthogonal zu der Tangente ?

Zunächst werden Einheitsvektoren berechnet, ein Einheitsvektor hat die Länge 1.

D.h. der Einheitsvektor zeigt die Richtung von q1, verbindet M1 und q1 nicht.

Sind meine Annahmen richtig?

VG Anna

---

Der Vektor d, ist der Verbindungsvektor zwischen M1 und M2 ?

Ja

Der Vektor n ist ein Normalenvektor, das heißt dieser Vektor ist orthogonal zu der Tangente ?

Ja

Zunächst werden Einheitsvektoren berechnet, ein Einheitsvektor hat die Länge 1.

auch Ja!

D.h. der Einheitsvektor zeigt die Richtung von q1, verbindet M1 und q1 nicht.

Ein Einheitsvektor $n$ (rot) zeigt vom Mittelpunkt $M$ zum Berührpunkt $q$. Siehe Skizze oben in meiner Antwort.

---

Vielen Dank! Ich habe eine Zeichnung dazu gemacht, ich wollte sichergehen, dass ich es richtig verstanden habe.

Answer 2

Zeichne eine Gerade g durch die Mittelpunkte der zwei Kreise.

Zeichne die zwei Senkrechten s₁ und s₂ zu g durch die Mittelpunkte der zwei Kreise.

Schnittpunkt von s₁ mit einem Kreis sei p₁. Schnittpunkt von s₂ mit dem anderen Kreis sei p₂. p₁ und p₂ müssen auf der gleichen Seite von g liegen.

Zeichne die Gerade h durch p₁ und p₂ ein.

Haben die Kreise den gleichen Radius, dann ist h Tangente an beiden Kreisen.

Haben die Kreise unterschiedlichen Radius, dann sei m der Schnittpunkt von h und g.

Konstruiere die Tangete des einen Kreises durch m. Diese ist auch Tangente des anderen Kreises.

Wie kann man auf einfachste Weise äussere Tangenten zweier Kreise berechnen?

Ich kenne nicht alle Wege, die äussere Tangenten zweier Kreise berechnen. Ich kann deshalb nicht beurteilen, ob mein Weg der einfachste ist.

Comments

Das soll nicht zeichnerisch sondern rechnerisch gelöst werden.

---

Ich bin davon ausgegangen, dass du die Konstruktion in eine Rechnung übersetzen kannst.

Answer 3

Ich nehme im Folgenden an, dass die Radien der Kreise r₁ und r₂ sowie der Abstand m der Mittelpunkte gegeben sind. Lege das so in ein Koordinatensystem:

Der größere Kreis sei K₁ mit dem Mittelpunkt (0|0) und dem Radius r₁, der kleinere Kreis sei K₂ mit dem Mittelpunkt M(m|0) und dem Radius r₂. Ein Kreis K₃ um (0|0) habe den Radius d=r₁ - r₂. Dann wird c bestimmt mittels c²+d²=m². Die Kreise (x-m)²+y²=c² und x²+y²=d² schneiden sich in P(u|v). Die Gerade mit der Steigung v/u durch den Punkt (m|0) schneidet K₂ in Q.  Die Gerade mit der Steigung v/u durch den Punkt (0|0) schneidet K₁ in R. Die Gerade QR ist dann Tangente.

Comments

Danke für die Antwort, die Tangenten sollen für verschiedene Kreise berechnet werden. Auch für Kreise, die nicht im Mittelpunkt des Koordinatensystem liegen. Ich habe zwar einen Rechenweg, aber die Tangenten haben nicht die richtigen Winkel.

Ich probiere diesen Ansatz.

---

Von zwei gegebenen Kreisen lässt sich immer einer so legen, dass sein Mittelpunkt der Ursprung des Koordinatensystems ist und der zweite lässt sich dann so legen, dass sein Mittelpunkt auf der x-Achse liegt.

Was soll hier als gegeben angesehen werden? War meine Annahme richtig, dass die Radien der Kreise r₁ und r₂ sowie der Abstand m der Mittelpunkte gegeben sind?  

Answer 4

Tangentensteigung:

$\frac{\sqrt{-v^2+12v-11}-\sqrt{9-u^2}}{v-u}$

$x^2+y^2=9$ → $y^2=9-x^2$  → $y=\sqrt{9-x^2}$  →    $y(u)=\sqrt{9-u^2}$

$y'(u)=\frac{-u}{\sqrt{9-u^2}}$

$\frac{\sqrt{-v^2+12v-11}-\sqrt{9-u^2}}{v-u}=\frac{-u}{\sqrt{9-u^2}}$

Mit Wolfram berechnet:

$u=-1$   und $v=\frac{13}{3}$

Comments

Ich verstehe aus mehreren Gründen den Sinn deiner Antwort nicht.

Erstens: Mit an Sicherheit grenzender Wahrscheinlichkeit interressiert sich die Fragestellerin nicht mehr dafür.

Zweitens: Deine Antwort liegt qualitativ weit hinter den bereits gegebenen Antworten. (Falls sich die Fragestellerinn tatsächlich noch für das Thema interessieren würde: Was nutzen ihr deine beiden ausgedachten Kreise mit deinen ausgedachten Mittelpunkten und deinen ausgedachten Radien?). Hast du ernsthaft geglaubt, dass deine Antwort hier irgendein Gewinn ist?

Als Drittes wäre dann noch dein Armutszeugnis

Mit Wolfram berechnet:

wobei ich mir sowieso nicht vorstellen kann, dass bei Eingabe der einen Gleichung mit zwei Variablen eine konkrete Lösung ausgespuckt wurde.

---

Wolfram zu nutzen, finde ich nun nicht schlimm. Aber eine nicht nachvollziehbare Antwort zu liefern, vor allem kommentarlos, schon.

---

Aber eine nicht nachvollziehbare Antwort zu liefern, vor allem kommentarlos, schon.

Ich kann mir nicht vorstellen, dass du die Antwort nicht nachvollziehbar findest.

---

Es geht aber nicht um mich. Und wie du an die beiden Berührpunkte gekommen bist, ist völlig unklar.

Diese "arrogante" Denkweise ist übrigens mit ein Grund, warum viele Mathelehrer schlechte Pädagogen sind (besonders die im Quereinstieg): sie gehen alle davon aus, dass die Schüler ihre Rechnungen problemlos nachvollziehen können. Kaum einer besitzt die Fähigkeit, das mal aus einer anderen Perspektive zu betrachten.

---

Was Moliets außerdem verschwiegen hat: wolframalpha zeigt MEHRERE mögliche Lösungspaare an. Vermutlich hat M. bei der Angabe "seines" Paares nur geschaut ob das optisch passen könnte und sich keine Gedanken gemacht ob (oder wenn nicht, warum) die anderen Paare auch zu möglichen gemeinsamen Tangenten führen oder eben nicht.

---

Und wie du an die beiden Berührpunkte gekommen bist, ist völlig unklar.

Ein Schüler, der solcher Art Aufgaben zum Lösen erhält, weiß bestimmt, wie er die Steigung einer Geraden über die 2 Punkteform der Geraden finden kann.

Ebenso kann er mit 2 Geraden die Schnittpunkte mit den beiden Kreisen finden, welche dann eben auch die Berührpunkte darstellen. Die Geraden durch diese beiden Punkte ist dann die Tangente.

(Zu meiner Zeit, vor über 65Jahren, waren die Konstruktion der äußeren wie auch inneren Tangenten Themen im Matheunterricht. Also nichts mit Berechnung.)

Somit gibt es auch einen weiteren Weg zur Berechnung der Tangenten.( siehe Roland.)

Also 1. Konstruktion und danach Lösungswege zur Berechnung.

---

Ich rechne mal mit der Konstruktionsbeschreibung (ist mir neu gewesen) von oswald:

$k_1:x^2+y^2=25$  und  $k_2:(x-6)^2+y^2=9$

1.)Zeichne eine Gerade g durch die Mittelpunkte der zwei Kreise:

$g: y=0$

2.)Zeichne die zwei Senkrechten s1 und s2 zu g durch die Mittelpunkte der zwei Kreise:

$s_1:x=0$    $s_2:x=6$

3.)Schnittpunkt von s1 mit einem Kreis sei p1. Schnittpunkt von s2 mit dem anderen Kreis sei p2. p1 und p2 müssen auf der gleichen Seite von g liegen.

$k_1: p_1=±5$   und $k_2: p_2=±3$  jeweils nur die oberen Koordinaten:
$p_1(0|5)$  und  $p_2(6|3)$

3.) Zeichne die Gerade h durch p1 und p2 ein.

$h: \frac{3-5}{6-0}=\frac{y-5}{x-0}$

$h: y=-\frac{1}{3}x+5$
4.)

Haben die Kreise den gleichen Radius, dann ist h Tangente an beiden Kreisen:

Ist hier nicht der Fall.

5.)Haben die Kreise unterschiedlichen Radius, dann sei m der Schnittpunkt von h und g.

$hXg: 0=-\frac{1}{3}x+5$    $m(15|0)$

6.)Konstruiere die Tangente des einen Kreises durch m.

Mitte von $\overline{M_1,m}$: $x=7,5$

Thaleskreis: $(x-7,5)^2+y^2=56,25$ schneidet  $k_1:x^2+y^2=25$:

$(x-7,5)^2+25-x^2=56,25$ in den beiden Berührpunkten der Tangenten:

$x^2-15x+\frac{225}{4}+25-x^2=\frac{225}{4}$

$x= \frac{25}{15}=\frac{5}{3}$    $(\frac{5}{3})^2+y^2=25$

 $y=±\frac{1}{3}\sqrt{200}=±\frac{10}{3}\sqrt{2}$

Nun die beiden Tangenten über die 2 Punkteform der Geraden berechnen:

$\frac{y_2-y_1}{x_2-x_1}= \frac{y-y_1}{x-x_1}$