Aufgabe:
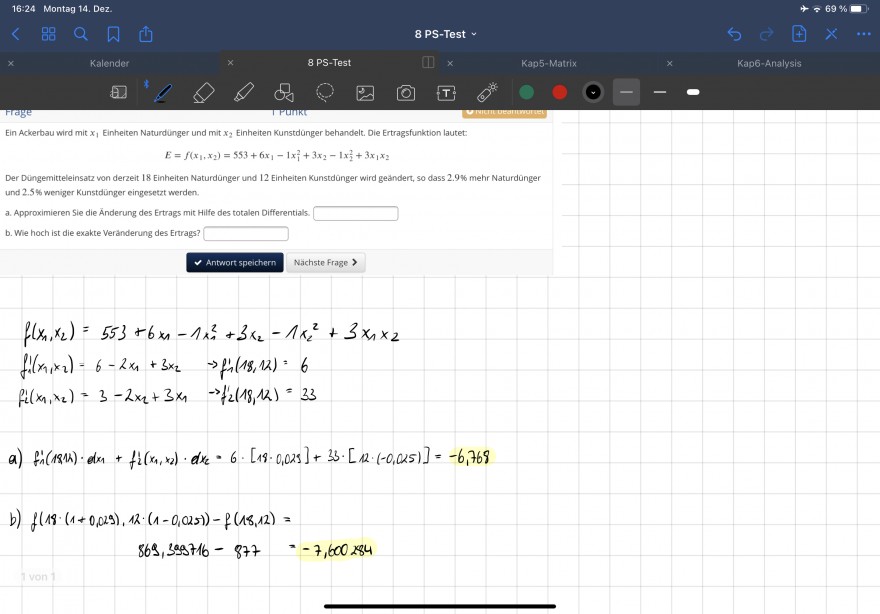
Text erkannt:
20
$$ E=f\left(x_{1}, x_{2}\right)=553+6 x_{1}-1 x_{1}^{2}+3 x_{2}-1 x_{2}^{2}+3 x_{1} x_{2} $$
We hoch ist die exakte Veranderung des Erruags?
$$ \begin{array}{l} f\left(x_{1}, x_{2}\right)=553+6 x_{1}-1 x_{1}^{2}+3 x_{2}-1 x_{2}^{2}+3 x_{1} \times 2 \\ f_{0}^{\prime}\left(x_{1}, x_{2}\right)=6-2 x_{1}+3 x_{2} \quad \rightarrow f_{1}^{\prime}(18,12)=6 \end{array} $$
\( f_{i}\left(x_{1}, x_{2}\right)=3-2 x_{2}+3 x_{1} \quad \rightarrow f_{2}(18,12)=33 \)
b) \( f(18 \cdot(1+0,029), 12 \cdot(1-0,025))-f(18,12)= \)
$$ 869,399716-877=-7,600 \times 84 $$
Ertragsfunktion - totales Differential und exakte Veränderung
Problem/Ansatz:
Habe diesen Lösungsweg hier auf mathelounge gefunden. Habe ich das so richtig gerechnet?