Hallo Gustavo,
mache Dir zunächst ein Bild des Problems: Die Nebenbedingung \(x+y+z=0\) kann man auch als eine Ebene im Raum auffassen, die durch den Ursprung verläuft. Ihr Normalenvektor \(\vec n\) wäre dann$$\vec n = \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}$$Die Nebenbedingung \(x^2+y^2+z^2 \le 1\) ist eine (Volll-)Kugel mit Mittelpunkt im Ursprung und dem Radius 1. Nimmt man die Schnittmenge dieser beiden Punktmengen, so bleibt eine Kreisscheibe mit Radius 1 und Normalenvektor \(\vec n\) übrig, wie hier im Bild zu sehen ist (die grüne Scheibe).
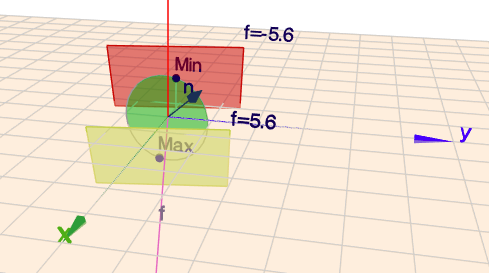
Die zu optimierende Funktion ist die lineare Funktion \(f(x,y,z)=5x+y-3z\), deren stärkster Anstieg in Richtung des lila Vektors \(\vec f\) verläuft. Die beiden eingezeichneten parallelen Ebenen sind jeweils Ebenen konstanten Wertes von \(f\). Die gelbe Ebene ergibt sich für \(f=4\sqrt{2} \approx 5,6\) und die rote für \(f = - 4\sqrt{2} \approx - 5,6\). Klicke oben auf das Bild, dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus rotieren und man bekommt einen besseren räumlichen Eindruck.
Beide Ebenen stehen senkrecht auf dem Vektor \(\vec f\) (lila)$$\vec f = \begin{pmatrix}5\\ 1\\ -3\end{pmatrix}$$Die Werte \(f = \pm 4\sqrt{2}\) sind so gewählt, dass sie die Kreisscheibe gerade noch berühen. Es ist es offensichtlich, dass die Berührpunkt \(B_{1,2}\) die gesuchten Extrema darstellen (Im Bild mit Min und Max bezeichnet). Durch relativ einfache geometrische Überlegungen kommt man zu$$B_1 = \frac 12\begin{pmatrix} \sqrt 2\\ 0\\ -\sqrt 2\end{pmatrix}, \quad B_2 = \frac 12\begin{pmatrix} -\sqrt 2\\ 0\\ \sqrt 2\end{pmatrix}$$Es gibt keinen Punkt \(\vec x\) auf der Kreisscheibe, bei dem der Wert \(f( \vec x) \) größer ist als bei \(\vec x = B_1\) und keinen Punkt bei dem der Wert für \(f(\vec x)\) kleiner ist als für \(\vec x = B_2\).
Ich berechne im folgenden die Extrema mit Hilfe des Lagrange-Multiplikator. Zunächst müssen wir die Ungleichung 'entschärfen'. Dazu nutze ich die Tatsache, dass \(f(x,y,z)\) eine lineare Funktion ist. Eine lineare Funktion hat keine lokalen Extrema, sonst wäre sie nicht linear! Folglich können die Extrema, wenn welche vorhanden sind, nur am Rand des Gebiets liegen, welches durch die Nebenbedingungen definiert ist. Also können wir das 'Inneren' der Scheibe vernachlässigen und untersuchen nur den Rand. Und für den gilt:$$x^2 + y^2 + z^2 = 1$$Mit dieser und der anderen Nebenbedingung kann man nun die Lagrange-Gleichung aufstellen und nach \(x\), \(y\) und \(z\) ableiten und Nullsetzen$$L(x,y,z,\lambda_1, \lambda_2)=5x+y-3z + \lambda_1(x^2+y^2+z^2-1) + \lambda_2(x+y+z)\\ \frac{\partial L}{\partial x} = 5 + 2\lambda_1 x + \lambda_2 = 0 \\ \frac{\partial L}{\partial y} = 1 + 2 \lambda_1 y + \lambda_2 = 0 \\ \frac{\partial L}{\partial z} = -3 + 2 \lambda_1 z + \lambda_2 = 0$$Subtraktion der ersten beiden Gleichungen führt zu$$5 + 2\lambda_1 x - 1 - 2 \lambda_1 y = 0 \implies \lambda_1 = \frac 2{y-x}$$Subtraktion der ersten und dritten Gleichung und Einsetzen von \(\lambda_1\) gibt$$5 + 2\lambda_1 x + 3 - 2 \lambda_1 z = 0 \\ 4 + \lambda_1(x-z) = 0 \\ \begin{aligned} \implies 4 + \frac 2{y-x}(x-z) &= 0 \\ z-x &= 2(y-x) \\ x - 2y + z &= 0\\ \end{aligned}$$Das sieht auf dem ersten Blick unspektakulär aus, ist aber hilfreich, wenn man von dieser Gleichung die Nebenbedingung \(x+y+z=0\) subtrahiert. Dann bleibt:$$-3y = 0 \implies y = 0$$Und damit folgt \(z=-x\). Einsetzen in die jetzt verbleibende Nebenbedingung \(x^2 +z^2 = 1\) gibt$$x = \pm \frac 12 \sqrt 2$$woraus dann wieder die beiden Punkte \(B_1\) und \(B_2\) folgen (s.o.).
Die aus der Rechnung gefundene Abhängigkeit \(x-2y+z=0\) ist nichts anderes als die Ebene, die durch \(\vec n\) und \(\vec f\) aufgespannt wird (s. Bild oben). Diese Ebene schneidet die Kreisscheibe und die Extrema liegen jeweils an den Enden des Schnittes.
Falls Du dazu noch Frage hast, so melde Dich bitte.
Gruß Werner