Vektoren und Skalarprodukt

Question

Aufgabe:

Im Buch steht die Lösung: AC * BC = 0, aber ich habe AC * AB = 0

Text erkannt:

10 Beschreiben Sie mithilfe geeigneter Skalarprodukte von allgemeinen Vektoren \( \overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}} \) usw, dass
a) das Dreieck \( \mathrm{ABC} \) bei C rechtwinklig ist,
b) das Dreieck \( \mathrm{ABC} \) bei A rechtwinklig ist,
c) das Viereck ABCD ein Rechteck ist,
d) das Viereck ABCD ein Quadrat ist.

Problem/Ansatz:

Text erkannt:

\( \Delta \)

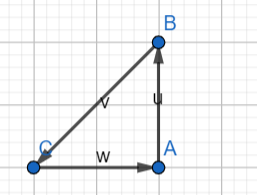
 => Meine Beschriftung

Warum liege ich hier Falsch? Oder liegt das an der Falschen Beschriftung des Dreiecks?

Answer 1

Aloha :)

Wenn du den Winkel an einem der Eckpunkte bestimmen möchtest, müssen beide Vektoren von diesem Eckpunkt aus starten. Damit bei \(C\) ein rechter Winkel liegt, muss also gelten:$$\overrightarrow{CA}\cdot\overrightarrow{CB}\stackrel!=0$$Die (didaktisch miserable) Lösung im Buch ist gleichwertig, denn es gilt:$$\overrightarrow{CA}=-\overrightarrow{AC}\quad;\quad\overrightarrow{CB}=-\overrightarrow{BC}$$Damit kannst du unsere Bedingung von oben umschreiben:$$0\stackrel!=\overrightarrow{CA}\cdot\overrightarrow{CB}=(-\overrightarrow{AC})\cdot(-\overrightarrow{BC})=\overrightarrow{AC}\cdot\overrightarrow{BC}$$

Answer 2

Oder liegt das an der falschen Beschriftung des Dreiecks?

Die Ecke mit dem rechten Winkel wird meistens C genannt. Aber was ist schon ein "falsche" Beschriftung?

Comments

Ja es gibt doch diese Grundregel wo man anfängt und dann gegen den Uhrzeigersinn alle anderen Ecken beschriftet, aber wusste nicht genau bei welcher Ecke man beginnen muss.

Answer 3

" a) das Dreieck ABC bei C rechtwinklig ist, "

" bei C rechtwinklig ist " bedeutet, dass gamma der rechte Winkel ist.

Deine Antwort passt aber zu b), denn 0 und -0 ist dasselbe. Daher brauchst du dich beim Resultat 0 nicht um das Vorzeichen zu kümmern, d.h. die Richtung des Pfeils ist egal.