Aufgabe: Ist diese Menge ein Vektorraum?

Question

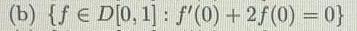
Text erkannt:

(b) \( \left\{f \in D[0,1]: f^{\prime}(0)+2 f(0)=0\right\} \)

Aufgabe: Ist diese Menge ein Vektorraum?

Problem/Ansatz:

Ich hab jetzt mit dieser Berechnung argumentiert, dass es ein Vektorraum ist.

\( \underbrace{f^{\prime}(0)+2 f(0)}_{0}+\lambda \cdot(g^{\prime} \underbrace{(0)+2 g(0))}_{0}=0 \)

Allerdings wenn ich die 2f(0) hinüber bringe steht da dann ja f'(0) = -2f(0) und meine neue Rechnung sähe nun so aus:

\( \underbrace{f^{\prime}(0)}_{-2 f(0)}+\underbrace{\lambda g ^{\prime}(0)}_{-2 f(0)} \stackrel{!}{=}-2 f(0) \) 

wenn ich Lambda nun als etwas absurd hohes wählen würde, kommt in dieser Addition ja niemals wieder -2f(0) heraus, oder? Ich hätte deswegen gemeint es ist kein Vektorraum.

Ich versteh deswegen nicht was ich hier falsch gemacht habe, da ich für beide Lösungen argumentieren könnte.

Answer 1

Allerdings wenn ich die 2f(0) hinüber bringe steht da dann ja f'(0) = -2f(0) und meine neue Rechnung sähe nun so aus:

\( \underbrace{f^{\prime}(0)}_{-2 f(0)}+\underbrace{\lambda g ^{\prime}(0)}_{-2 f(0)} + \lambda 2g (0) \stackrel{!}{=}-2 f(0)   \)

Comments

Wieso zählt man jetzt den Term lambda 2g(0) dazu? ich versteh aber trotzdem noch nicht inwiefern die Gleichung jetzt gelöst ist, mir kommt da dann einfach 0 = 0 heraus.

---

Wieso zählt man jetzt den Term lambda 2g(0) dazu?

Klammer korrekt auflösen !

ich versteh aber trotzdem noch nicht inwiefern die Gleichung jetzt gelöst ist, mir kommt da dann einfach 0 = 0 heraus.

Dann ist doch die Sache wahr.