Volumen und den Oberflächeninhalt

Question

Aufgabe:

Wie berechnet man das Volumen V  und den Oberflächeninhalt O einer regelmäßigen sechsseitigen
Pyramide mit der Grundkante und s

a= 6,25m   s=16,25m

…

Problem/Ansatz:

Answer 1

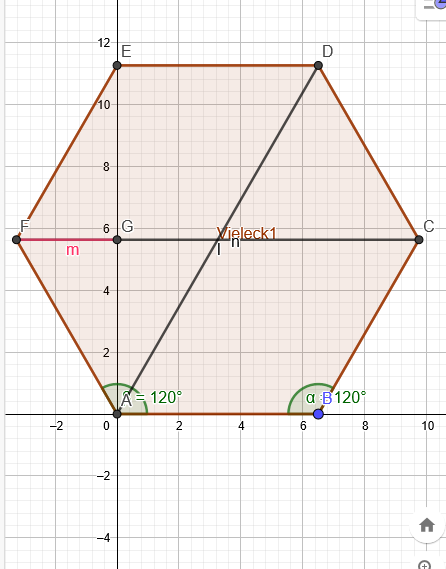
Grundfläche:

Die Grundfläche lässt sich in 2 gleich große Trapeze aufteilen

sin(30°)=\( \frac{Strecke F G}{Strecke F A} \)

Strecke F C=2 * Strecke F G + a

Höhe des Trapez  über Pythagoras oder tan (30°)

Eine Mantelfläche (gleichschenkliges Dreieck):

Die Diagonalen (Strecke A D und Strecke F C)der Grundfläche halbieren sich .

Weiter mit Pythagoras bezüglich der Höhe der Pyramide  und der Seitenkante s.

Wenn du nun die Höhe der Pyramide hast, kannst mit obigen Daten auch die Fläche des gleichschenkligen Dreiecks berechnen

Volumen :  \( \frac{1}{3} \)*G*h

Answer 2

Grundfläche: G=6·6,25²/4·√3

Pyramidenhöhe H=\( \sqrt{16,25^2-6,25^2} \)

Volumen V=1/3·G·H

Höhe einer Seitenfläche: h=\( \sqrt{16,25^2-3,25^2} \)

Seitenfläche S=\( \frac{6,25}{2} \)·\( \sqrt{16,25^2-3,25^2} \)

Oberfläche O=G+6·S