Von den Nullstellen auf die NF

Question

Aufgaben:

(1)

Gegeben sind die Nullstellen x1 = 2 und x2=5 sowie a=2. Stelle f(x) in Linearfaktordarstellung auf und bestimme den Scheitelpunkt S rechnerisch.

(2)

Gegeben sind die Nullstellen x1=4 und x2=-2 sowie a=0,5. Stelle f(x) in Linearfaktordarstellung auf und bestimme den Scheitelpunkt S rechnerisch.

Problem/Ansatz:

Kann mir jemand evlt. erklären wie ich von den Nullstellen auf die Normalformel/Allgemeinformel komme?

Bzw. mir evlt eine Aufgabe vorrechnen damit ich die andere alleine versuchen kann.

Vielen Dank im voraus!

Answer 1

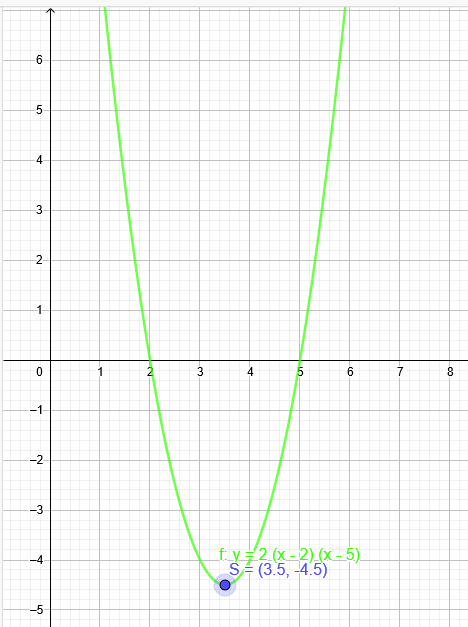
Gegeben sind die Nullstellen x₁ = 2 und x₂=5 sowie a=2. Stelle f(x) in Linearfaktordarstellung auf und bestimme den Scheitelpunkt S rechnerisch.

y=a*(x-N₁)*(x-N₂)

y=2*(x-2)*(x-5)

y=2x^2-14x+20|-20

y-20=2x^2-14x|:2

\( \frac{y-20}{2} \)=x^2-7x|+q.E.(\( \frac{-7}{2} \))^2=\( \frac{49}{4} \)

\( \frac{2y-40}{4} \)+\( \frac{49}{4} \)=x^2-7x+\( \frac{49}{4} \)

\( \frac{2y+9}{4} \)=(x-\( \frac{7}{2} \))^2|*4

2y+9=4*(x-\( \frac{7}{2} \))^2|-9

2y=4*(x-\( \frac{7}{2} \))^2-9|:2

y=2*(x-\( \frac{7}{2} \))^2-4,5

S(3,5|-4,5)

Comments

Wenn du schon Ableitungen gehabt hat, ist es da dann auch möglich S zu bestimmen.