analy.. geometrie dreieck

Question

Aufgabe:

Das Dreieck ABC ist ein gleichseitiges Dreieck, das in einen Kreis mit Radius 1 und Mittelpunkt (0|0) einbeschrieben ist. Der Punkt A hat die Koordinaten A(1|0).

1. Bestimmen Sie die Koordinaten von B und C.
2. Bestimmen Sie die Länge einer Dreiecksseite.
3. Bestimmen Sie den Flächennhalt des Dreiecks.

Lösungen:

Problem/Ansatz:

Hallo ich habe ein Problem bei oben stehender Aufgabe aus meinem Script. Die Lösung ist zwar vorhanden aber ich komme absolut nicht darauf, wie ich diese herleiten kann.

Bitte nach Möglichkeit ausführlich erklären.

Vielen Dank für Eure Hilfe im voraus

Answer 1

Hallo Kevin,

Willkommen in der Mathelounge!

Zeichne in dem Bild oben noch ein paar zusätzliche Strecken ein:

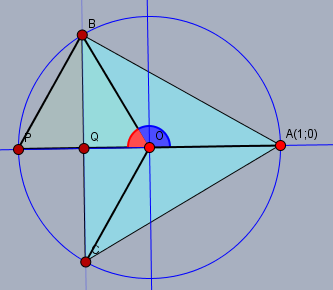
Der Koordinatenursprung sei der Punkt \(O\). Alle drei Strecken \(|OA|\), \(|OB|\) und \(|OC|\) haben die Länge des Radius des Kreises also \(1\). Da der Vollkreis durch diese drei Strecken in drei gleiche Winkel geteilt wird, muss einer dieser Winkel (blau) gleich \(120°\) sein. Und die Hälfte davon (der rote Winkel) demzufolge \(60°\).

Und da der rote WInkel \(60°\) ist und die Seite \(BC\) senkrecht auf der X-Achse seht, ist das rechtwinklige Dreieck \(\triangle QOB\) die Hälfte des gleichseitigen Dreiecks \(\triangle POB\).

Also ist $$|QO| = \frac 12 |PO| = \frac 12$$nun kann man mit Pythagoras im Dreieck \(\triangle QOB\) die Länge der Seite \(|QB|\) berechnen$$1^2 = |QB|^2 + \left( \frac 12\right)^2 \implies |QB|= \frac 12 \sqrt 3$$und da \(|BC| = 2|QB|\) ist, ist die Seitenlänge des blauen gleichseitigen Dreiecks$$|BC| = 2|QB| = 2 \cdot \frac 12 \sqrt 3 = \sqrt 3$$

ich denke, das reicht, um die Koordinaten und die Fläche des Dreiecks zu berechnen - oder? Falls noch Fragen offen sind, bitte melden.

Gruß Werner

Comments

Hallo Werner Vielen Dank für deine Hilfe :)

Answer 2

Moinsen

Sei B (x/y) dann ist auch C(x/-y)

Du brauchst zwei Gleichungen zur Lösung

Schau dir an wie der Abstand vom Mittelpunkt (0/0) zu den Punkten B A oder C im allgemeinen definiert ist und dann entspricht das genau dem Radius der Kugel.

Zweite Gleichung Stichwort Gleichseitig, also der Abstand von B zu C ist genauso lang wie der Abstand von A zu B ;) damit hast du deine zweite Gleichung

Der rest sollte kein Problem mehr sein

Answer 3

1.)Kreis um M(0|0) mit r=1:   x^2+y^2=1

Gerade durch  A(1|0) und B:

\( \frac{y-0}{x-1} \)=tan(150°)

y=tan(150°)*x-tan(150°)

Text erkannt:

\( y=-\frac{1}{\sqrt{3}} \cdot x+\frac{1}{\sqrt{3}} \)
\( y=-\frac{1}{3} \sqrt{3} \cdot x+\frac{1}{3} \sqrt{3} \)
\( x^{2}+y^{2}=1 \)
\( x^{2}+\left(-\frac{1}{3} \sqrt{3} \cdot x+\frac{1}{3} \sqrt{3}\right)^{2}=1 \)
\( x^{2}+\frac{1}{3} x^{2}-\frac{2}{3} x+\frac{1}{3}=1 \)
\( \frac{4}{3} x^{2}-\frac{2}{3} x=\frac{2}{3} \)
\( 4 x^{2}-2 x=2 \)
\( x^{2}-\frac{1}{2} x=\frac{1}{2} \)
\( \left(x-\frac{1}{4}\right)^{2}=\frac{1}{2}+\frac{1}{16}=\frac{9}{16} \mid \sqrt{ } \)
1.) \( x-\frac{1}{4}=\frac{3}{4} \)
\( x_{1}=1 \) kommt nicht in Frage.
2.) \( x-\frac{1}{4}=-\frac{3}{4} \)
\( x_{2}=-\frac{1}{2} \)
\( x^{2}+y^{2}=1 \)
\( \frac{1}{4}+y^{2}=1 \)
\( y^{2}=\frac{3}{4} \)
\( y_{1}=\frac{1}{2} \cdot \sqrt{3} \)
\( y_{2}=-\frac{1}{2} \cdot \sqrt{3} \)