Berechne die Koordinaten des Vektors x=[1,7,9] in dieser Basis.

Question

Aufgabe:

Betrachte den Vektorraum R^3

Vektoren :

a=[3,0,2]

b=[-8,-6,7]

c=[4,1,-9]

bilden eine Basis.

Berechne die Koordinaten des Vektors x=[1,7,9] in dieser Basis.

x= lambda1*a + lambda2*b +lambda3*c

lambda1=?

lambda2=?

lambda3=?

Kann mir jemand sagen, wie ich auf die lambda komme?

Answer 1

Hallo Carla,

das ist nichts anders als die Lösung eines linearen Gleichungssystems. In Matrix-Schreibweise$$\begin{pmatrix}3& -8& 4\\ 0& -6& 1\\ 2& 7& -9\end{pmatrix} \cdot \begin{pmatrix}\lambda_1\\ \lambda_2\\ \lambda_3\end{pmatrix} = \begin{pmatrix}1\\ 7\\ 9\end{pmatrix}$$mit der etwas krummzahligen Lösung$$\begin{pmatrix}\lambda_1\\ \lambda_2\\ \lambda_3\end{pmatrix} = -\frac{1}{173} \begin{pmatrix}117\\ 270\\ 409\end{pmatrix} \approx \begin{pmatrix}-0.6763\\ -1.5607\\ -2.3642\end{pmatrix}$$

Das Bild zeigt es graphisch. Die Linearkombination aus \(a\), \(b\) und \(c\) führt zum Vektor \(x\) (schwarz)

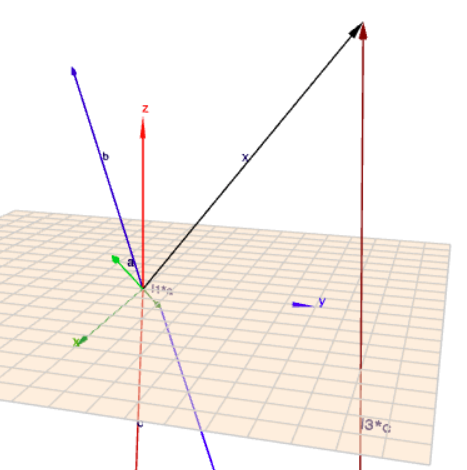
(klick auf das Bild, dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus rotieren und bekommst einen besseren Eindruck)

Gruß Werner