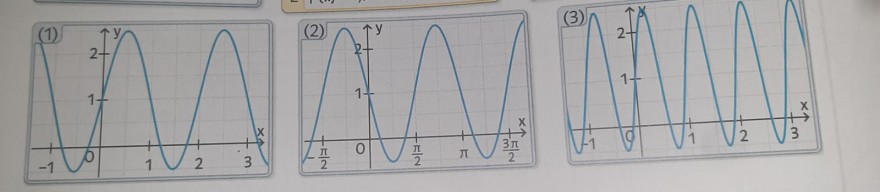
Aufgabe: Finden Sie die beiden Funktionsterme, die zu jeweils einem der Graphen (1) bis (3) passen.
A: f(x) = 1,5 * sin(2*(x-π/2)) + 1
B: f(x) = -1,5 * sin(π * (x+1)) + 1
C: f(x) = 1,5 * sin(π * x+2π) + 1
D: f(x) = 1,5 * sin(2π * (x+1)) +1
E: f(x) = 1,5 * sin(2π *(x-1)) + 1
F: f(x) = - 1,5 * sin(2*(x-π)) + 1