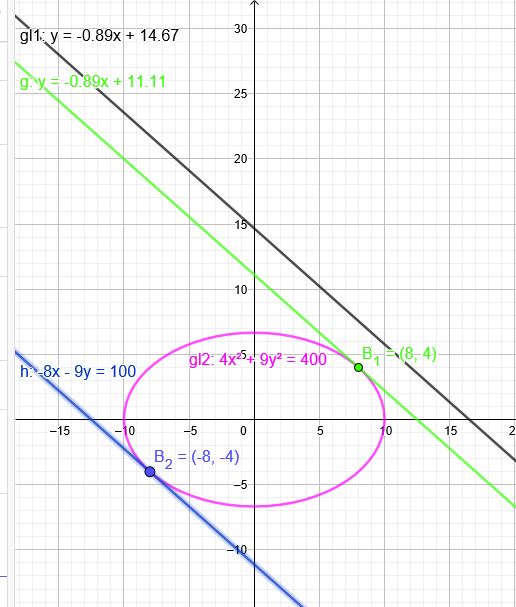
Bestimme jene Tangenten an die Ellipse ell, die zur Geraden g parallel sind. Gib auch die Koordinaten der Berührpunkte an.
g: \(8x + 9y = 132\) → \(y=\red{-\frac{8}{9}}x+\frac{132}{9}\)
ell: \(4x^2 + 9y^2 = 400\)
\(e(x,y)=4x^2 + 9y^2 - 400\)
\(e_x(x,y)=8x\)
\(e_y(x,y)= 18y\)
\(e'(x)=-\frac{e_x(x,y)}{e_y(x,y)}=-\frac{8x}{18y}=-\frac{4x}{9y}\)
\(\red{-\frac{8}{9}}=-\frac{4x}{9y}\)
\(y=\frac{1}{2}x\) schneidet die Ellipse in den beiden Berührpunkten der Tangenten:
\(4x^2 + \frac{9}{4}x^2 = 400\)
\(x_1=8\) \(y_1=4\)
\(x_2=-8\) \(y_2=-4\)
Nun mit einem geeigneten Verfahren die beiden Tangenten berechnen.