Gauß-Verteilung zeigen, dass es keine ist

Question

Text erkannt:

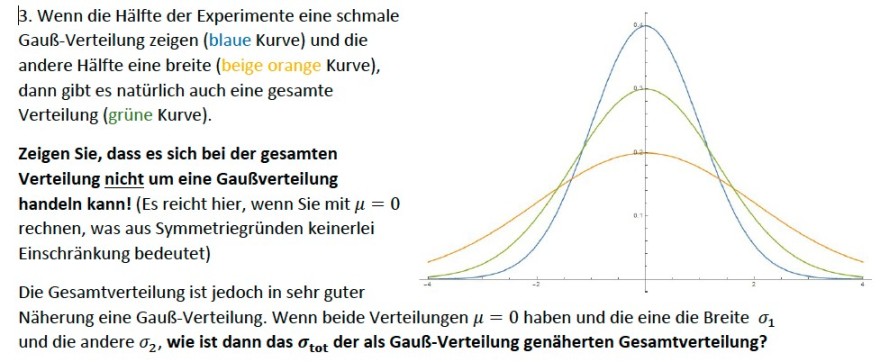
Gauß-Verteilung zeigen (blaue Kurve) und die
andere Hälfte eine breite (beige orange Kurve),
dann gibt es natürlich auch eine gesamte
Verteilung (grüne Kurve).
Zeigen Sie, dass es sich bei der gesamten
Verteilung nicht um eine Gaußverteilung
handeln kann! (Es reicht hier, wenn Sie mit \( \mu=0 \)
rechnen, was aus Symmetriegründen keinerlei
Einschränkung bedeutet)
Die Gesamtverteilung ist jedoch in sehr guter
Näherung eine Gauß-Verteilung. Wenn beide Verteilungen \( \mu=0 \) haben und die eine die Breite \( \sigma_{1} \)
und die andere \( \sigma_{2} \), wie ist dann das \( \sigma_{\text {tot }} \) der als Gauß-Verteilung genäherten Gesamtverteilung?

Comments

Solange keine Kriterien genannt werden, wann eine Näherung als "sehr gut"  bezeichnet werden darf, schlage ich für σ_tot das harmonische Mittel von σ₁ und σ₂ vor.