Aufgabe:
Bereche f´(2).
Problem/Ansatz:
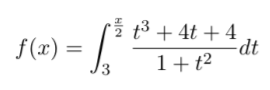
Text erkannt:
\( f(x)=\int \limits_{3}^{\frac{x}{2}} \frac{t^{3}+4 t+4}{1+t^{2}} d t \)
Was ich mir überlegt habe: man kann beide Seiten derivieren, da die Funktion für beide Grenzen stetig ist.
dann bekomme ich f´(x)=(t3+4t+4)/1+t2
Wenn ich dann 2 einsetze, bekomme ich ein falsches Ergebnis. Man soll auf 9/4 kommen. Was mache ich falsch? Wie soll man da vorgehen?
Danke