Wie diese komplexe Menge skizzieren?

Question

Hallo, ich hab folgendes Problem:

Skizzieren Sie die Menge \( \mathcal{A}=\{z \in \mathbb{C}:|z| \leq 2\} \) und das Bild von \( \mathcal{A} \) unter der Funktion
\( f: \mathbb{C} \rightarrow \mathbb{C}, \quad z \mapsto \operatorname{Re}(z)+2+\frac{i}{2} \operatorname{Im}(z) \)

Wie man A skizziert ist mir klar. Ein Kreis mit M(0/0) und r= 2. Aber wie funktioniert das mit f(A)?

Danke im voraus.

Answer 1

Lösung mit cartesischen Koordinaten.

Es ist \(f(x+iy)=u+iv\) mit \(u=x+2\) und \(v=y/2\),

also \(x=u-2,\; y=2v\). Dann hat man: $$x^2+y^2\leq 4 \iff (u-2)^2+4v^2 \leq 4 \iff \frac{(u-2)^2}{2^2} + \frac{v^2}{1^2}\leq 1.$$Das ist eine Ellipse mit Mittelpunkt \((2|0)\) und den Halbachsen

\(a=2, \; b=1\).

Answer 2

Aloha :)

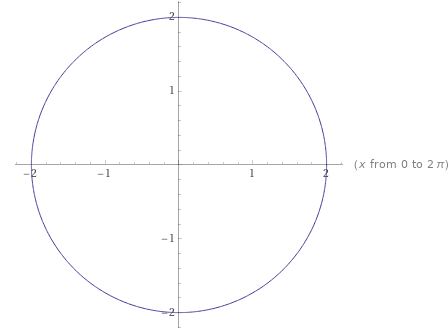
Alle \(z\in A\) bilden in der Gauß'schen Zahlenebene eine Kreisscheibe mir Radius \(2\) um den Ursprung (inklusive des Randes):$$z=\binom{r\cos\varphi}{r\sin\varphi}\quad;\quad r\in[0;2]\;;\;\varphi\in[0;2\pi]$$

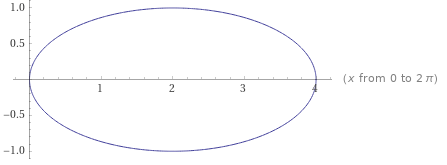
Die Abbildungsvorschrift lautet in Koordinatenschreibweise:$$f(z)=\operatorname{Re}(z)+2+\frac i2\,\operatorname{Im}(z)=\binom{\operatorname{Re}(z)+2}{\frac12\operatorname{Im}(z)}=\binom{r\cos\varphi+2}{\frac r2\sin\varphi}=\binom{2}{0}+r\binom{\cos\varphi}{\frac 12\sin\varphi}$$

Das ist eine Ellipse um den Mittelpunkt \((2|0)\) mit großer Halbachse \(a=2\) und kleiner Halbachse \(b=1\):