Hallo,
ich unterstelle mal, dass die Lichtquelle bei der Position \(L=(2|0|10)\) liegt, so wie es im Punkt c) Deiner Aufgabe gefordert ist. Und weiter gehe ich davon aus, dass der Schatten des Turms auch wirklich zeichnerisch konstruiert werden soll und nicht berechnet und dann in die Zeichnung eingetragen!
Wichtig: Es können nur Flächen Schatten werfen, die auch beleuchtet werden. Und wenn die Lichtquelle oben links im Bild liegt, dann wird z.B. der Punkt \(F\) nicht beleuchtet und gehört damit auch zu keiner Fläche, die einen Schatten produziert.
Letztlich spielen für den Schatten nur die vier Flächen in dem Fünfeck \(ACGSE\) eine Rolle. Und da \(A\) und \(C\) ihre eigenen Schattenpunkte sind - \(A=A'\) und \(C=C'\) - bleiben nur die drei Punkte \(G\), \(S\) und \(E\), deren Projektionen zeichnerisch ermittelt werden müssen.
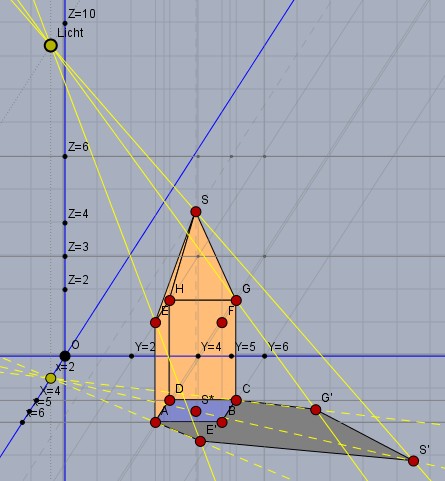
Man konstruiert einen Schattenpunkt indem man die Gerade durch den Lichtpunkt \(L\) und den Orignalpunkt - z.B. \(S\) - zeichnet (gelb im Bild) und diese Gerade mit der Gerade (gelb gestrichelt) durch die Projektion \(L^*\) auf die Grundfläche - hier \(L^*=(2|0|0)\) - mit der Projektion \(S^*\) - hier \(S^*=(5|5|0)\) - zum Schnitt bringt. Der Schnittpunkt \(S'\) ist dann die Projektion von \(S\) durch \(L\) auf die Grundfläche.
Genauso verfährt man mit den Punkten \(E\) und \(G\). Hier ist \(E^*=A\) und \(G^*=C\). Der 'fertige' Schatten ist dann das Fünfeck \(AE'S'G'C\). Falls Du Fragen hast, so melde Dich bitte.
Gruß Werner