Uns wurde die Aufgabe gestellt sämtliche Lösungen folgender beider Komplexen Zahlen zu finden:

Wie es mit komplexen Zahlen der Form z=a+b*i (a und b ungleich 0) funktioniert habe ich verstanden, jedoch komme ich bei diesen Zahlen einfach nicht weiter. Anbei meine Lösungsversuche bzw. Probleme:
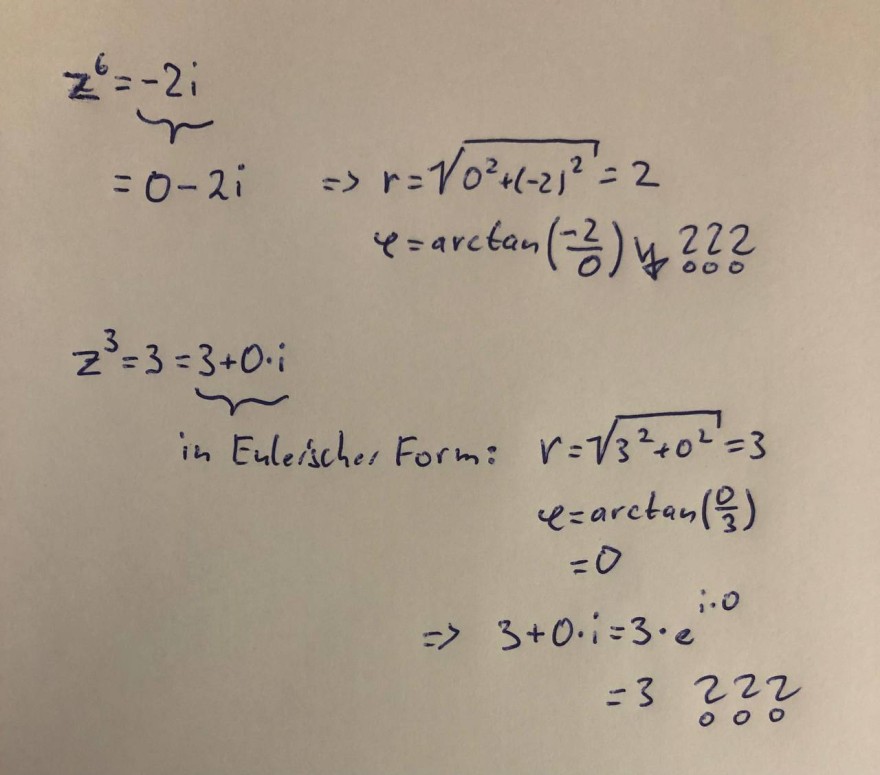
Könnt ihr mir vielleicht weiterhelfen?