\(f´(t)=200* e^{-0,01 t}-2*(t-15)*e^{-0,01 t} \)
\(f´(t)= e^{-0,01 t}*(200-2*t+30) \)
\(f´(t)= e^{-0,01 t}*(230-2*t) \)
\(f´´(t)= e^{-0,01 t}*(-0,01)*(230-2*t)+ e^{-0,01 t}*(-2) \)
\(f´´(t)=e^{-0,01 t}*(-2,3+0,02t-2)\)
\(f´´(t)=e^{-0,01 t}*(0,02t-4,3)\)
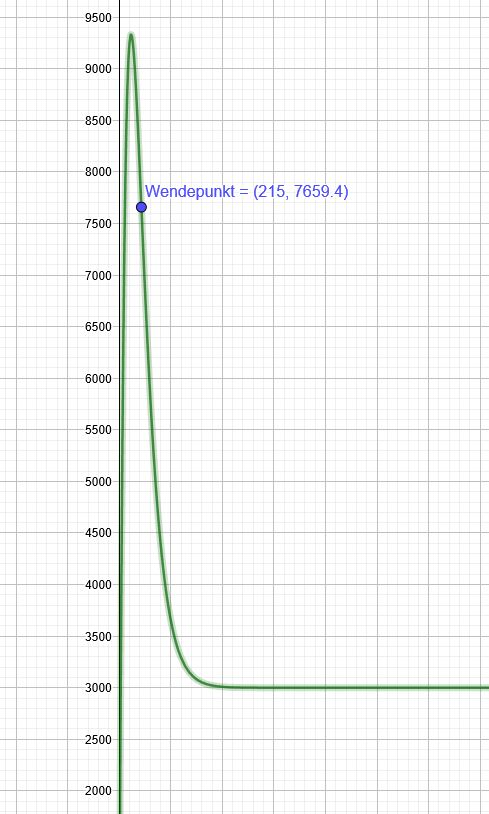
\((0,02t-4,3)=0\) → \(t=215\)
\(f(215)=200 *(215-15) * e^{-0,01 *215}+3000 ≈7659,4\)
Die 3.Ableitung brauchst du nicht.