ne, schau nochmal 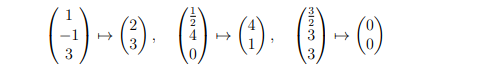
Text erkannt:
\( \left(\begin{array}{c}1 \\ -1 \\ 3\end{array}\right) \mapsto\left(\begin{array}{l}2 \\ 3\end{array}\right), \quad\left(\begin{array}{l}\frac{1}{2} \\ 4 \\ 0\end{array}\right) \mapsto\left(\begin{array}{l}4 \\ 1\end{array}\right), \quad\left(\begin{array}{l}\frac{3}{2} \\ 3 \\ 3\end{array}\right) \mapsto\left(\begin{array}{l}0 \\ 0\end{array}\right) \)
das sind zwar alles v`s aber da steht nicht welches welches ist, aber klar wäre logisch, dass das erste v1 usw. ist
aber wieso gilt dann \(v_1+v_2=v_3\) , also wieso muss unbedingt, der erste Vektor zsm addiert mit dem 2. den dritten ergeben?