(x^4 + 7·x^3 - 208·x^2 + 980·x - 1200):(x-2)=x^3+9x^2-190x+600
-(x^4-2x^3)
........................
9x^3 - 208·x^2
-(9x^3 - 18x^2)
--------------------------
-190x^2+980·x
-(-190x^2+380x)
-------------------------------------
600x-1200
-(600x-1200)
---------------------------------------
0
(x^3+9x^2-190x+600):(x-5)=x^2+14x-120
-(x^3-5x^2)
-------------------
14x^2-190x
-(14x^2-70x)
.....................
-120x+600
-(-120x+600)
.............................
0
x^2+14x-120=0
x^2+14x=120
(x+7)^2=120+49=169
1.) x+7=13
x₁=6
2.) x+7=-13
x₂=-20
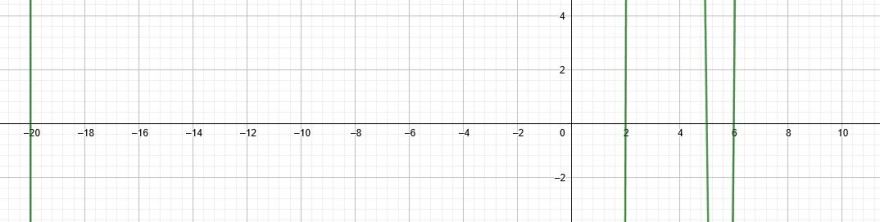
Nullstellen: -20,2,5,6