Aufgabe:bestimme die gesuchte Fläche

Text erkannt:
\( \int \limits_{1}^{2}\left(e^{-2 t}+1\right) d t \quad \) Zuerst die Hochzahion berechner
\( =\left[-\frac{1}{2} e^{-2 t}+t_{1}^{2}=\left(-\frac{1}{2} e^{-2 \cdot 2}+2\right)-\left(\frac{1}{2} e^{-2}+1\right)=\frac{1}{2} e^{-x}+2+\frac{1}{2} e^{-2}+1\right. \)
Problem/Ansatz:
Hallo Ich bräuchte wieder Hilfe undzwar weiß ich erstmal nicht ob das alles was nach der stammfunktion kommt überhaupt richtig ist aber falls ja dann wäre meine frage was mache ich wie wo mit den hoch zahlen die nach dem zweiten gleichzeitigen kommen? Denn da steht ja: "1/2e‐^4+2+1/2s‐²+1" und wenn ich das ganze "normal" mit dem Taschenrechner berechne dann habe ich als Ergebnis = 23 aber in meinem "Mathe buch" steht als Ergebnis = 1,059FE. ich weiß nicht wo ich falsch gegangen bin und wieso das eigentliche Ergebnis 1,059FE ist und könnte mit jemand auch sagen für was nochmal FE steht? Beihand lege ich noch ein Foto hinzu vom der Aufgabe fall meine Schrift nicht gut zu erkennen ist.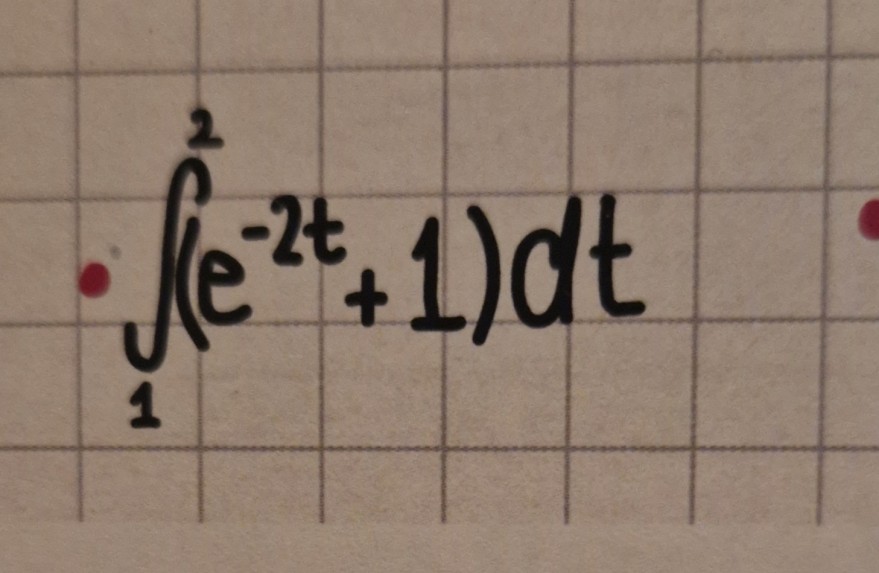
Text erkannt:
\( \cdot \int \limits_{1}^{2}\left(e^{-2 t}+1\right) d t \)
LG und danke schonmal.im voraus