Aloha :)
Du kannst das Problem ummünzen auf die Suche von Nullstellen der Funktion$$f(x)\coloneqq x^3-\sqrt{|x|}+e^x-3$$Man sieht schnell, dass \(f(1)=e-3<0\) und \(f(2)=5-\sqrt2+e^2>0\) ist. Da die Funktion stetig ist, muss sie eine Nullstelle im Intervall \((1;2)\) besitzen. Wir beschränken uns bei der Nullstellensuche auf dieses Intervall, sodass wir die Betragszeichen unter der Wurzelfunktion weglassen dürfen:$$f(x)=x^3-\sqrt x+e^x-3\stackrel!=0\quad;\quad x\in(1;2)$$
Zur konkreten Bestimmung der Nullstelle verwenden wir das Newton-Verfahren. Das heißt, wir starten mit einem Schätzwert\(x_0\in(1;2)\) und legen die Tangente durch diesen Punkt an den Graphen von \(f(x)\):$$t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)$$Die Nullstelle dieser Tangente$$0\stackrel!=t(x)\quad\implies\quad x=x_0-\frac{f(x_0)}{f'(x_0)}$$wählen wir dann als neuen Schätzwert für die Nullstelle. Wir berechnen also:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\quad;\quad x_0=\text{Schätzwert}$$solange, bis wir das Ergebnis mit der gewünschten Genauigkeit erhalten.
Wir wählen als ersten Schätzwert die Mitte unseres Intervalls \(x_0=1,5\). Zum Glück ist die Ableitung nicht schwierig zu bilden, sodass:$$x_{n+1}=x_n-\frac{x_n^3-\sqrt{x_n}+e^{x_n}-3}{3x_n^2-\frac{1}{2\sqrt{x_n}}+e^{x_n}}\quad;\quad x_0=1,5$$
Ab hier habe ich Tante Excel mit dem Rechnen beauftragt:
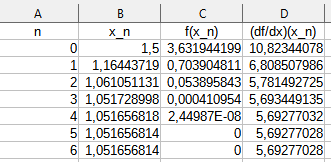
Die gesuchte Nullstelle liegt also bei \(x\approx1,051656814\).