Aufgabe:
Von 6 verschiedenen Geschenken werden 4 auf 4 Kinder verteilt
Problem/Ansatz:
Die Lösung sagt, dass die mit Reihenfolge ohne Wiederholung berechnet werden muss, als
6*5*4*3. Ich verstehen nicht wieso mit Reinfolge, weil ich hätte jetzt erst 4 aus 6 gerechnet und dann die Möglichkeiten 4 Geschenke aus 6 zu ziehen als n und k also die 4 Kinder ohne Wiederholung mit Reihenfolge berechnet.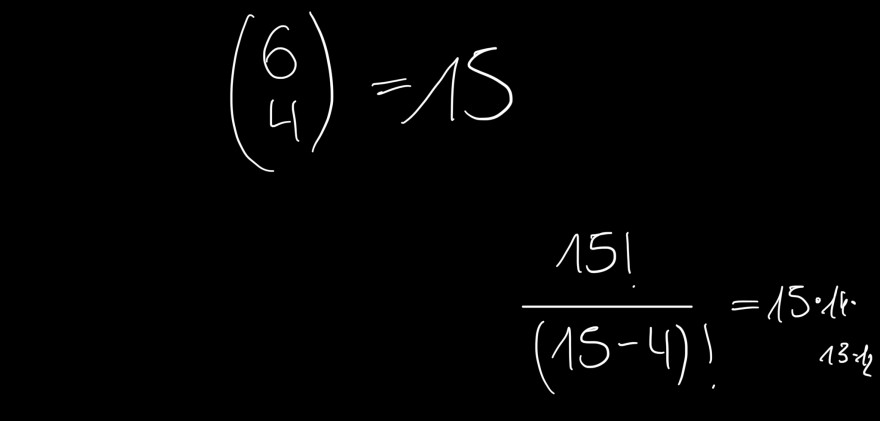
Text erkannt:
\( \begin{array}{l}\left(\begin{array}{l}6 \\ 4\end{array}\right)=15 \\ \qquad \frac{15 !}{(15-4) !}=15 \cdot k k+13 k 4\end{array} \)
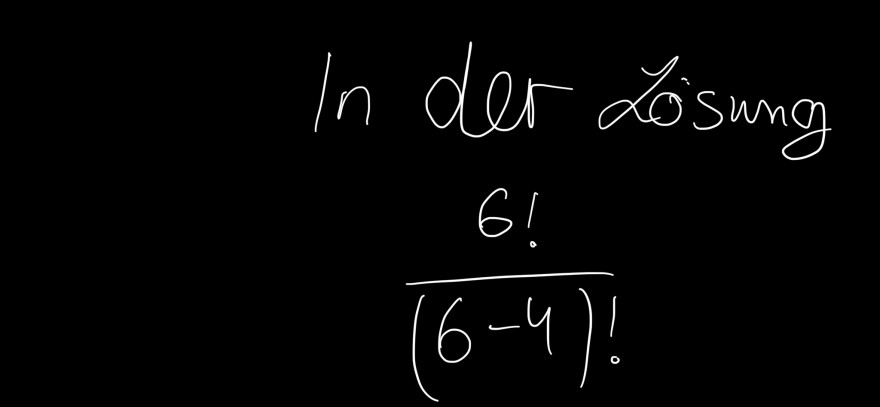
Text erkannt:
In der Losung
\( \frac{6 !}{(6-4) !} \)