Links-rechts-Wendepunkte?

Question

Ich hab da mal eine Frage:

nehmen wir mal an ich hab die Funktion f(x)=x³-6x²+9x und möchte die Wendepunkte bestimmen. Das hab ich in dem Fall schon getan und hab den (richtigen!) Wendepunkt W(2I2). Nun möchte ich aber wissen ,ob dieser ein Links-rechts-Wendepunkt oder ein Rechts-links-Wendepunkt ist. Dafür bildet man ja die dritte Ableitung der Funktion(in diesem Fall : f'''(x)=6) und setzt dann für x die zuvor errechnete Stelle also hier 2 ein. Nun ist in der dritten Ableitung aber kein x vorhanden. Wie erkenne ich nun, ob dies ein Rechts-links-Wendepunkt oder ein Links-rechts-wendepunkt ist?

Answer 1

 

f(x) = x³ - 6x² + 9x

f'(x) = 3x² - 12x + 9

f''(x) = 6x - 12

f'''(x) = 6

 

Wendepunkt:

f''(x) = 0 ∧ f'''(x) ≠ 0

6x - 12 = 0 | x = 2

f'''(2) = 6 ≠ 0

Also Wendepunkt W(2|f(2)) = W(2|2)

 

Bis dahin kommen wir also auf das gleiche Ergebnis :-)

 

 

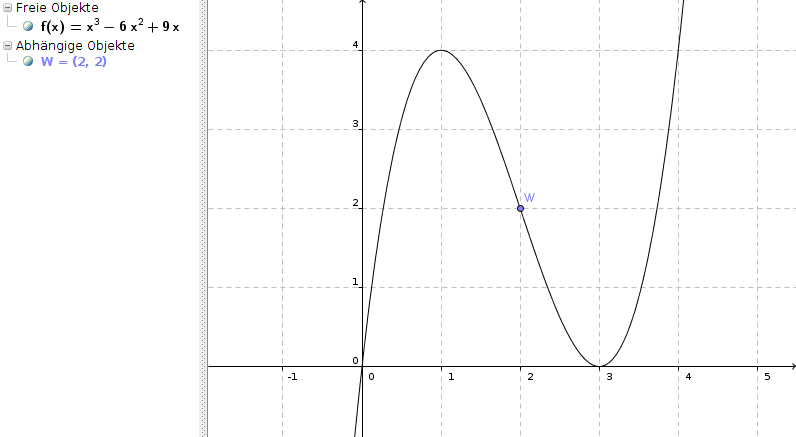
Der Skizze entnehmen wir, dass es ein Rechts-links-Wendepunkt ist.

Im Wendepunkt ist bekanntermaßen der Betrag des Anstiegs maximal.

Ich weiß auch nicht genau, wie man jetzt feststellen kann, um welche Art eines Wendepunktes es sich handelt.

Eine Idee:

Man setzt einen etwas kleineren x-Wert und einen etwas größeren x-Wert als den gefundenen (hier x = 2) in die 1. Ableitung ein, zum Beispiel:

f'(1,9) = 3 * 1,9² - 12 * 1,9 + 9 = -2,97

f'(2,2) = 3 * 2,2² - 12 * 2,2 + 9 = -2,88

Wir haben also an beiden Stellen einen negativen Anstieg, der aber nach rechts hin "weniger negativ" ist; das dürfte ein Hinweis darauf sein, dass es sich um einen Rechts-links-Wendepunkt handelt.

Ist wie gesagt nur eine Idee, aber es lohnt sich m. E., diese in Betracht zu ziehen :-)

 

Besten Gruß

Comments

Es gibt die Bedingung:

für f'''(x)>0 haben wir einen Rechts-Links-Wendepunkt.

und andersrum.


Wenn nach rechts-links bzw. links-rechts gefragt wird, ist diese Bedingung sicher bekannt ;).

---

@Unknown:

Das macht Sinn und ist wesentlich ökonomischer als meine Idee!

In meiner Mini-Formelsammlung (als App auf meinem Handy), mit der ich gemeinhin prima auskomme, ist diese Regel nicht aufgelistet :-((

Danke Dir mal wieder!!!

---

Kannst gleich eine Beschwerde an den App-Verantwortlichen schicken :D.


Im Ernst: Ist keine oft gefragte Bedingung und auch nicht verwunderlich, dass nicht gelistet ;).


Gerne :)

---

Dankeschön. Hab es jetzt dank eurer Konversation verstanden :) mfg

---

Das freut uns!!

Und: Gern geschehen :-)

Answer 2

Hi,

für f'''(x)>0 haben wir einen Rechts-Links-Wendepunkt.

Da 6>0 ist, liegt genau dieser vor ;).


Grüße