Aufgabe:
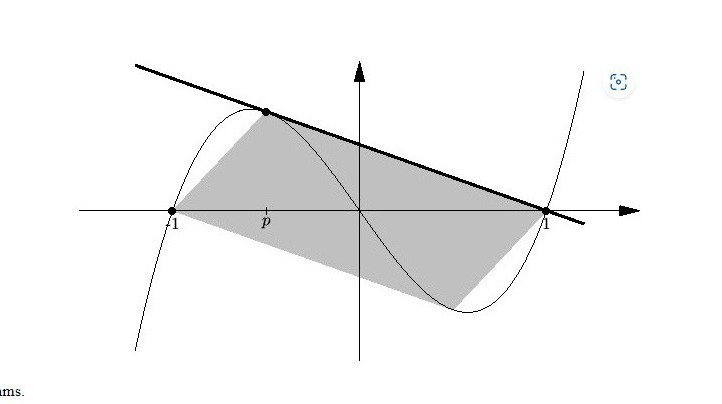
Gerade und Polynom, Flächeninhalt eines Parallelogramms
Die Gerade berührt den Graph des Polynoms für x=p und schneidet für x=1 den Graphen senkrecht.
Bestimmen Sie b, s, p und a sowie den Flächeninhalt des markierten Parallelogramms.
y=sx+b, s<0
y=a(x2+x)(x-1)
Problem/Ansatz:
b=? s=? p=(-0.5) a=?
y=a(x2+x)(x-1) wird zu y=ax3-ax
Dafür setze ich p=(-0.5) ein um die Höhe in Abhängigkeit von a zu erhalten.
f(-0,5) = a(-0,5)3-a(-0,5)
f(-0,5)=0,375a
Nun berechne ich die Steigung der Geraden.
m=\( \frac{y2-y1}{x2-x1} \) = \( \frac{0,375a-0}{-0,5-1} \) = \( \frac{0,375a}{-1,5} \) = -0,25a
Als Geradenfunktion erhalte ich und berechne mit dem Punkt P(0,375/-0,5) den y-Achsenabschnitt
f(x)=-0,25ax+b
0,375a=-0,25a (-0,5) + b
0,375a=0,125a+b / -0,125
0,25a=b
Da ich jetzt b=0,25a kenne, folgt die Geradengleichung in Abhängigkeit von a
f(x) = -0,25ax+0,25a
Das Polynom und die Gerade schneiden einander und teilen sich beide den Punkt P(-0,5/0,375a), sodass ich die beiden Funktionen gleichsetzen kann, um a=? zu erhalten?
ax3-ax = -0,25ax+0,25a / +0,25ax
ax3-ax+0,25ax = 0,25a / setze für x=-0,5 ein
0,25 = 0,25a / :0,25
a=1
Wenn a=1, dann sollte folgendes richtig sein???? b=0,25 s=(-0,25) p=(-0,5) a=1
Das Parallelogramm habe ich mit den Längen berechnet wenn a=1
A1=1,5*0,375=0,5625
A2=0.5*0,375=0,1875
A1+A2=Ages
Ages= 0,75
Vielleicht kann jemand meine Ergebnisse überprüfen bzw. mir ein Feedback geben, was ich falsch und/ oder richtig gemacht habe.
Leider habe ich kein Lösung und das Onlinetool sagt mir ständig meine Lösung ist falsch bis auf p=(-0,5)......
Danke. LG