Berechne die Krümmung von dem Vektor

Question

Aufgabe:

Berechne die Krümmung von γ:R->R³ 

^{γ(t)= $\begin{pmatrix} cost\\sint\\t \end{pmatrix}$}

^{in jedem t∈R.}  

Comments

Berechne die Krümmung von dem Vektor

Der hat keine.

Answer 1

Hallo,

gesucht ist die Krümmung der (Raum-)Kurve $\gamma(t)$ und nicht die des Vektors.

Bevor man das berechnet, sollte man sich diese Kurve mal veranschaulichen. Die ersten beiden Koordinaten bilden einen Einheitskreis, der alle $2\pi$-mal einmal durchlaufen wird. Die dritte Koordinate ist schlicht eine lineare Abbildung von $t$. Folglich gibt das ganze eine Spirale (eigentlich Schraublinie) mit einem Innendurchmesser von $1$.

Stellt man sich die Spirale abgerollt vor, so legt $t$ alle $2\pi$-mal die Strecke von $\sqrt{2}\cdot 2\pi$ zurück und die Krümmung ist überall konstant. Da die Krümmung $\kappa$ die Inverse des Radius des Krümmungskreises der Bahnkurve ist, kann man daraus bereits schließen, dass $\kappa$ konstant und kleiner $1$ ist.

Die Rechnung ergibt:$$\begin{aligned} \gamma'(t) &= \begin{pmatrix}-\sin(t)\\ \cos(t)\\ 1\end{pmatrix}, \quad \gamma''(t)=\begin{pmatrix} -\cos(t)\\ -\sin(t)\\ 0\end{pmatrix}\\ \kappa(t) &= \frac{\left| \gamma'(t) \times \gamma''(t)\right|}{\left| \gamma'(t)\right|^3} \\ &= \frac{1}{\left(\sqrt{\sin^2(t) + \cos^2(t) + 1}\right)^3} \left| \begin{pmatrix}-\sin(t)\\ \cos(t)\\ 1\end{pmatrix} \times \begin{pmatrix} -\cos(t)\\ -\sin(t)\\ 0\end{pmatrix}\right| \\ &= \frac{1}{\left(\sqrt{\sin^2(t) + \cos^2(t) + 1}\right)^3} \left| \begin{pmatrix}\sin(t)\\ -\cos(t) \\ \sin^2(t)+\cos^2(t)\end{pmatrix} \right| \\ &= \frac{\sqrt{2}}{(\sqrt{2})^3} = \frac{1}{2}\end{aligned}$$siehe Krümmung für parametresierte Kurven.

Comments

Nachtrag:

ich hatte anfangs vermutet, dass die Krümmung $1/\sqrt{2}$ betragen müsste. Deshalb war ich über das Ergebnis $\kappa=1/2$ etwas überrascht und war mir nicht sicher, ob die Rechnung (s.o.) korrekt ist. Inzwischen weiß ich aber, wo mein Denkehler war ;-)

Zur Verfizierung des Ergebnisses habe ich den Krümmungskreis (grün) mit der Krümmung $\kappa=1/2$ im Punkt $(1,\,0,\,0)$ in Geoknecht eingetragen.

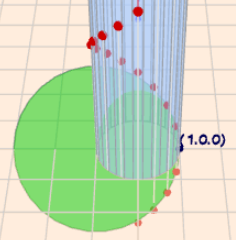
Die Schraubline $\gamma(t)$ ist als Punktfolge (rot) dargestellt, die sich an der Wand eines Zylinders (blau) entlang schlängelt (klick auf das Bild).

Genauer sieht man es in Desmos aus der gleichen Perspektive in die Ebene des Krümmungskreises projiziert:

Der Kreis (grün) mit der Krümmung $\kappa=1/2$ bzw. Radius $r=2$ passt sich der Schraublinie (rot) genau an. Die Krümmung $\kappa=1/\sqrt{2}$ des gestrichelt dargestellten Kreises ist dagegen zu groß.