Schade! Jetzt hat wieder jemand aus meinem Kommentar eine Antwort gemacht. Das sollte aber gar keine Antwort sein!!
Ihr habt natürlich Recht. Was einfach und was schwierig ist, ist natürlich äußerst subjektiv zu beurteilen. Allerdings fände ich das schon interessanter und dem Niveau hier auch angemessen, den Schwierigkeitsgrad etwas zu steigern.
Deshalb hier mein Vorschlag die Frage zu 'pimpen':
Eine quadratische Fläche ist vollständig und überdeckungsfrei von bunten Rechtecken bedeckt. Alle Rechtecke haben den identischen Flächeninhalt. Die Längeneinheit \(1\text{LE}\) ist rechts unten angegeben, nebst dem Flächeneinheit \(1\text{FE}\) in Form eines schwarzen Quadrates außerhalb der eingangs erwähnten quadratischen Fläche rechts unten im Bild.
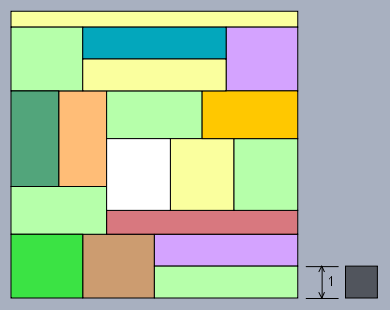
Frage: Wieviele Flächeneinheiten fasst die quadratische Fläche aus den bunten Rechtecken?
Hinweis: Es gibt Rechtecke, die wie Quadrate aussehen ...
Gruß Werner