Wieso darf ich hier nicht die 0 einsetzen sondern muss mit x^3 erweitern?

Question

Aufgabe: Bestimmen Sie die folgenden Grenzwerte

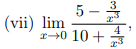
Text erkannt:

(vii) \( \lim \limits_{x \rightarrow 0} \frac{5-\frac{3}{x^{3}}}{10+\frac{4}{x^{3}}} \),

Problem/Ansatz:

Ganz kurze Frage: Wieso darf ich hier nicht die 0 einsetzen sondern muss mit x^3 erweitern? Ich hätte ja nicht durch 0 geteilt. Gibt es da noch irgendeine Regel woran ich das erkenne?

Answer 1

Ganz kurze Frage: Wieso darf ich hier nicht die 0 einsetzen.

Ganz kurze Antwort. Im Nenner eines Bruches darf NIE Null stehen, weil man durch 0 nicht teilen darf! Ich verstehe nicht wie du denken kannst das du dann nicht durch Null teilen würdest.

Tipp das doch so als Aufgabe mal in den Taschenrechner ein indem du x mit 0 ersetzt und schau ob der Taschenrechner das ausrechnen kann.

Comments

Ich dachte wegen der 10 im Nenner wäre das ok. Weil der gesamte Nenner dann nicht 0 wäre... Aber jetzt verstehe ich, der Bruch darf auch nicht einfach durch 0 geteilt werden.

Danke für die ganz kurze Antwort :D

---

Dass der Nenner nicht Null werden darf, gilt für jeden Bruch. Du hast in deinem Term drei Brüche und in jedem darf der Nenner nicht Null werden.

---

$$\lim\limits_{x \to 0} \frac{5-\frac{3}{x^3}}{10+\frac{4}{x^3}} \newline \text{mit } x^3 \text{ erweitern.} \newline \lim\limits_{x \to 0} \frac{5x^3-3}{10x^3+4} = -\frac{3}{4}$$

---

Ja stimmt, danke.

Answer 2

Weil der Nenner für x= 0 nicht definiert ist.

Für x gegen gehen die Brüche gegen + oo bzw. -oo, je nach Annäherung von rechts oder links.

Man bildet den Hauptnenner und kürzt x^3 raus. (Doppelbruchgesetz)

Comments

Ja danke dir für deine Antwort.