Sei f:R^2→R^2
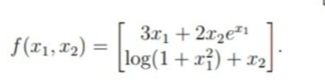
Text erkannt:
\( f\left(x_{1}, x_{2}\right)=\left[\begin{array}{c}3 x_{1}+2 x_{2} e^{x_{1}} \\ \log \left(1+x_{1}^{2}\right)+x_{2}\end{array}\right] \).
Auf welchen Bereich ist f^-1 definiert? Da die Berechnung von der Umkehrfunktion in diesen Fall alles andere als trivial ist, denke ich, dass man per Intuition entscheiden soll wo diese definiert ist. Die erste als auch zweite Komponente kann theoretisch jeden reellen Wert annehmen, demnach würde ich sagen, dass die Umkehrfunktion auf ganz R^2 definiert ist. Liege ich damit richtig?
Text erkannt:
\( f\left(x_{1}, x_{2}\right)=\left[\begin{array}{c}3 x_{1}+2 x_{2} e^{x_{1}} \\ \log \left(1+x_{1}^{2}\right)+x_{2}\end{array}\right] \).