In unserem Skript und dem Forster Lehrbuch sind die Definitionen für die taylorformel/Taylorpolynom einw enig unterschiedlich:
Unsere Formel:
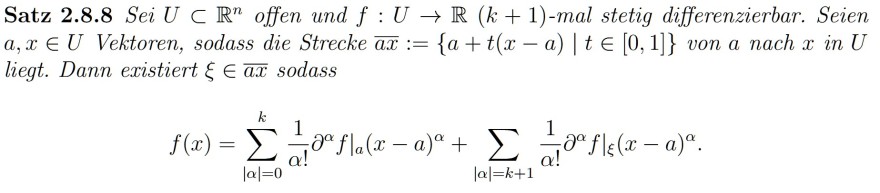
Lehrbuch Forster:
Text erkannt:
Satz 2.8.8 Sei \( U \subset \mathbb{R}^{n} \) offen und \( f: U \rightarrow \mathbb{R}(k+1) \)-mal stetig differenzierbar. Seien \( a, x \in U \) Vektoren, sodass die Strecke \( \overline{a x}:=\{a+t(x-a) \mid t \in[0,1]\} \) von a nach \( x \) in \( U \) liegt. Dann existiert \( \xi \in \overline{a x} \) sodass
\( f(x)=\left.\sum \limits_{|\alpha|=0}^{k} \frac{1}{\alpha!} \partial^{\alpha} f\right|_{a}(x-a)^{\alpha}+\left.\sum \limits_{|\alpha|=k+1} \frac{1}{\alpha!} \partial^{\alpha} f\right|_{\xi}(x-a)^{\alpha} . \)
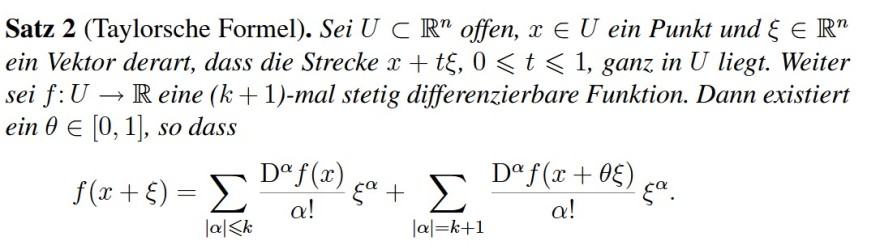
Text erkannt:
Satz 2 (Taylorsche Formel). Sei \( U \subset \mathbb{R}^{n} \) offen, \( x \in U \) ein Punkt und \( \xi \in \mathbb{R}^{n} \) ein Vektor derart, dass die Strecke \( x+t \xi, 0 \leqslant t \leqslant 1 \), ganz in \( U \) liegt. Weiter sei \( f: U \rightarrow \mathbb{R} \) eine \( (k+1) \)-mal stetig differenzierbare Funktion. Dann existiert \( \operatorname{ein} \theta \in[0,1] \), so dass
\( f(x+\xi)=\sum \limits_{|\alpha| \leqslant k} \frac{\mathrm{D}^{\alpha} f(x)}{\alpha!} \xi^{\alpha}+\sum \limits_{|\alpha|=k+1} \frac{\mathrm{D}^{\alpha} f(x+\theta \xi)}{\alpha!} \xi^{\alpha} . \)
Zum EInen ist mir bis jetzt noch nicht ganz klar, wieso man auf der einen Seite ein \(\xi\) nutzt, welches zwischen 0 und 1 liegt und auf der anderen Seite \((x-a)^\alpha\). Zumal der Entwicklungspunkt a, den wir so definiert haben, in der zweiten Definition des Polynom gar nicht vorkommt?
Außerdem ist es mir noch unklar, wieso man einmal nur f(x) nimmt und einmal \(f(x+\xi)\), weiß das jemand?
Zum Anderen kenne ich bis jetzt nur diese \(\partial^{\alpha}\) für die partiellen Ableitungen und nicht \(D^{\alpha}\), ist damit das gleiche gemeint?
Vielen Dank im Voraus!