Stimmt meine Fallunterscheidung? |x^2 - 4x + 3| ≥ 1.

Question

Hallo :)
Habe bei einer Fallunterscheidung Schwierigkeiten. Ich glaube es liegt auch daran, dass ich den Betrag falsch aufgelöst habe
Hier die Aufgabe: 


Zuerst habe ich den Betrag aufgelöst.


Stimmt das -(x²-4x+3) <3 für x <3 und x>1?
Beim 1. Fall habe ich keine Probleme.  Da erhalte ich einmal x ≤ 2-√2 und x≥ 2+√2.
Nun zum 2. Fall...  ich habe x≤2 erhalten. Aber das kann doch nicht stimmen. Wenn ich Werte die größer sind als 2 einsetze, dann erhalte ich auch einen Wert der kleiner als 1 ist.  Ich hab mir schon überlegt, dass eventuell es für den 2. Fall lautet x <3, da ja 3>2. Naja, meine jetzige Lösungsmenge lautet : L= (-∞,2]∪[2+√2,∞) Danke für die Antworten.

Answer 1

Die Lösungsmenge Ist  {x∈ℝ | x = 2 ∨ x ≤ 2 - √2 ∨ x ≥ √2 + 2 }

du bist nahe dran!

Gruß Wolfgang

Answer 2

Dein 1.Fall ist richtig.

2. Fall gilt für 1 < x < 3
( x^2 -4x + 3) * ( -1) ≥ 1 | * (-1)
x^2 - 4x + 3 ≤ -1 
x^2 - 4x + 3 + 1 ≤ -1 + 1
( x -2 )^2 ≤ 0
Quadrate sind immer größer / gleich 0
x - 2 = 0
x = 2

Für die 2.Fall heißt die Lösung x = 2

Comments

Danke für den 2. Fall :)

Ich weiß leider nie, wann ich 1 < x <3 nehmen soll. Warum kann ich nicht mit x>1, x<3 rechnen?

Danke für die Antwort.

---

Ich weiß leider nie, wann ich 1 < x <3 nehmen soll.
Warum kann ich nicht mit x>1, x<3 rechnen?

Das ist dasselbe.

( x größer 1 ) und (  x < 3 ) heißt :
x liegt zwischen 1 und 3

Mache dir den Sachverhalt am Zahlenstrahl klar.
Zahlenstrahl aufmalen
Punkte 1 und 3 eintragen.
Die Bereiche x < 1 und x > 3 einzeichnen.

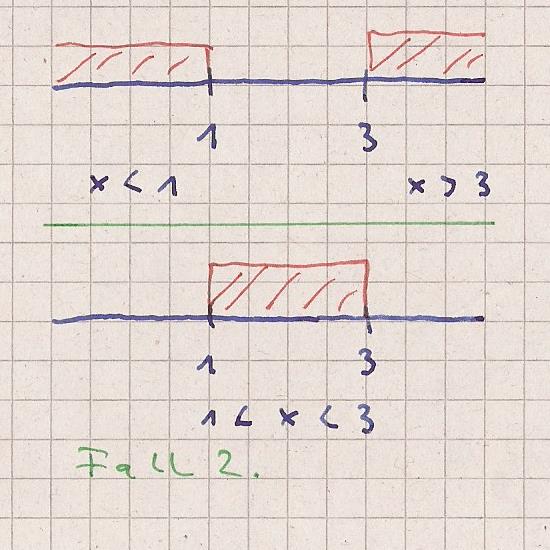
Der Bereich der übrig bleibt ist der Bereich dazwischen.

x liegt zwischen 1 und 3 : 1 < x < 3

Auch bei den Lösungen kann ein Zahlenstrahl die Bereiche
oder Schnittmengen verdeutlichen.

Ich hoffe ich habe deine Frage richtig verstanden und konnte
dir weiterhelfen.

Ansonsten frag bitte nach.

Oder stelle eine weitere Frage ein.

mfg Georg

---

Danke ! Jetzt wurde es mir klar :)

Habe aber eine weitere Frage- Warum wurde am Anfang mit (-1) multipliziert?

Den Rest verstehe ich :)

---

x^2 - 4 * x + 3   ist positiv falls ( x < 1 ) und ( x > 3 )

x^2 - 4 * x + 3   ist negativ falls   1 < x <  3

Dies ist dann Fall 2

| x^2 - 4 * x + 3 |  ≥ 1
Die Betragszeichen bedeuten : falls x^2 - 4 * x + 3 negativ ist
gilt dafür die Funktion
( x^2 - 4 * x + 3 ) * (-1 )
dann wird der Ausdruck ins Positive umgedreht ( Betrag )
und das Relationszeichen ≥ bleibt erhalten.
( x^2 - 4 * x + 3 ) * (-1)   ≥ 1

---

Tut mir leid für diese späte Antwort .

Das im 2.Fall x <0 gilt weiß ich und auch das was du mir erklärt hast, verstehe ich.

Im 2. Fall multipliziert du aber dann noch einmal mit (-1). Das Ungleichszeichen wird umgedreht.

Warum  machst du diesen Schritt?  Darauf wäre ich nie gekommen. Ich hätte einfach mit -x²+4x-3 weiter gerechnet. Muss man das einfach sehen, dass  man hier mit (-1) multipliziert muss?

Danke für deine Antworten :) Du hilfst mir echt weiter :)

---

Ungleichungen / Betragsgleichungen können etwas verwirrendes
haben.

Ich gehe meistens nach " Schema f " vor und bin damit auf
der sicheren Seite.

| term | ( Betrag von term, abs () , stets positiv einzusetzen )

In allen weiteren mathematischen Berechnungen ist einzusetzen

falls term > 0 kann mit term weitergerechnet werden

falls term < 0 kann mit term * ( -1 )  weitergerechnet werden ohne
das sich in den Gleichungen etwas ändert.
( Die Multiplikation mit ( -1 ) verwandelt einen negativen Wert in einen positiven )
Mir ist dies lieber als Relationszeichen umzudrehen.