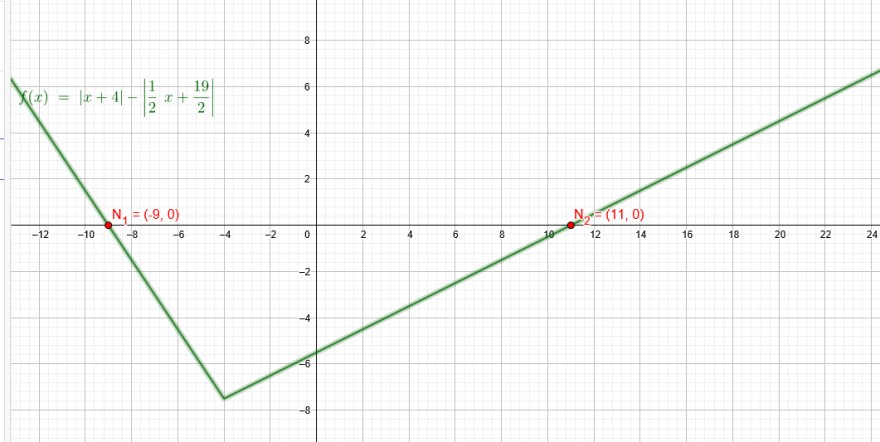
|x+4| = |\( \frac{1}{2} \) x + \( \frac{19}{2} \)|
Quadrieren:
(x+4)^2=(\( \frac{1}{2} \) x + \( \frac{19}{2} \))^2
(x+4)^2-(\( \frac{1}{2} \) x + \( \frac{19}{2} \))^2=0
[x+4+(\( \frac{1}{2} \) x+\( \frac{19}{2} \))]*[x+4-(\( \frac{1}{2} \) x+\( \frac{19}{2} \))]=0
x+4+\( \frac{1}{2} \) x+\( \frac{19}{2} \)=0
x₁=-9
x+4-(\( \frac{1}{2} \) x+\( \frac{19}{2} \))=0
x₂=11