Ich generiere mal eine Antwort und versuche meine Konstruktion auch rechnerisch zu optimieren, quick and dirty;-). Dazu lasse ich den Solver f(r,h,dx) auf die Abwicklung mit dem Startpunkt E0 los:
α=ARCTAN(r / SQRT(4*h^2 + 3*r^2))*2
E0=(dx, 0)
E1=(dx + r, 0)
...
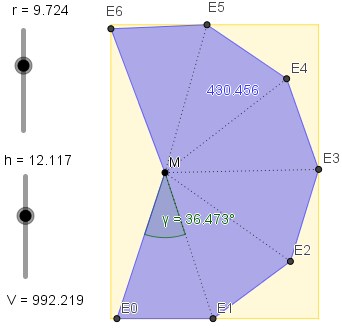
E(i)=E(i-1) + r (sin((180° - 2(i-1)α) / 2), cos((180° - 2(i-1)α) / 2))
V=r^2 *SQRT(3)*h / 2 ====> max
in den Nebenbedingungen achte ich darauf, dass die Koordinaten der Eckpunkte E(i)=(x,y) innerhalb des DINA4-Bereiches bleiben: 0<=x<=21, 0<=y<=29,7.
Damit komme ich auch auf das "leicht schräg" liegende Abwicklungsbild, allerdings nicht auf die von Werner und Gast hj2166 versprochenen Volumina.
Bin mal gespannt, wo da noch Platz für mehr Raum ist...