Aufgabe:
Text erkannt:
Winkelfunktionen
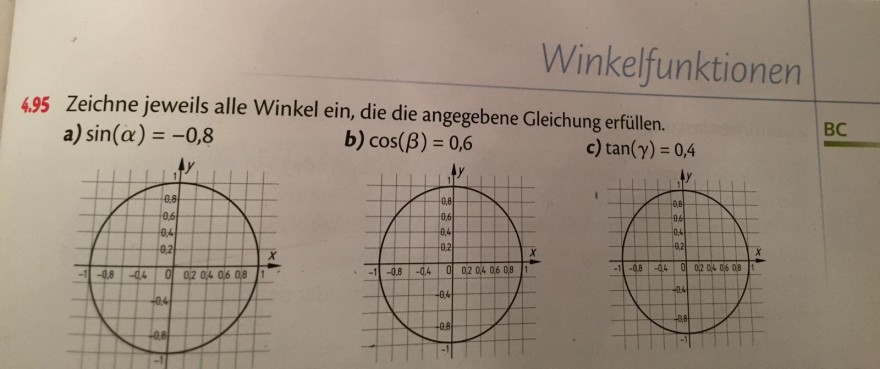
4.95 Zeichne jeweils alle Winkel ein, die die angegehene
a) \( \sin (\alpha)=-0,8 \)
b) \( \cos (\beta)=0,6 \)
c) \( \tan (\gamma)=0,4 \)
Problem/Ansatz: Anbei sieht die Lösungen aus dem Lösungsheft...
Text erkannt:
4.95 a)
b)
c)
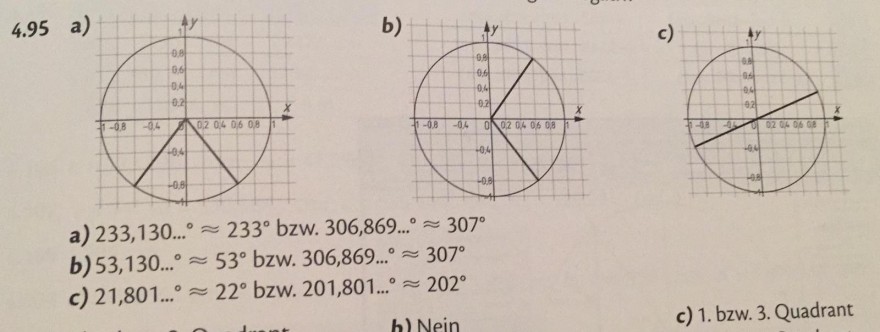
a) \( 233.130 \ldots^{\circ} \approx 233^{\circ} \mathrm{bzw} .306,869 \ldots^{\circ} \approx 307^{\circ} \)
h) \( 53130 \% \approx 53^{\circ} \) bzw. \( 306,869 \ldots^{\circ} \approx 307^{\circ} \)
c) 1. bzw. 3. Quadrant
Ich verstehe nicht wie man auf die Lösung kommt? Was ist der Lösungsweg? Warum werden in den Lösungen jeweils zwei Winkel als Lösung angegeben? Im Falle des Beispiels 4.95)a sind jeweils 233 Grad und 307 Grad als Lösung angegeben? Wieso ist das so? Ich wäre euch sehr dankbar, wenn ihr mir bei dieser Aufgabe helfen könntet!
LG Ben