Wir betrachten die \( \mathrm{Ba} \) sis \( \mathcal{B}=\left(b_{1}, b_{2}, b_{3}\right) \) des \( \mathbb{R}^{3} \) mit
$$ b_{1}=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right), \quad b_{2}=\left(\begin{array}{l} 0 \\ 1 \\ 1 \end{array}\right), \quad b_{3}=\left(\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right) $$
Sei \( f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) diejenige lin eare Abbildung, die
$$ f\left(b_{1}\right)=b_{2}, \quad f\left(b_{2}\right)=b_{3}, \quad f\left(b_{3}\right)=b_{1} $$
erfüllt
(a) Sei \( \mathcal{E}=\left(e_{1}, e_{2}, e_{3}\right) \) die kanonische Basis des \( \mathbb{R}^{3} \). Bestimmen Sie die darstellenden Matrizen des Ba siswech sels \( M_{\mathcal{E}}^{\mathcal{B}} \) und \( M_{\mathcal{B}}^{\mathcal{E}} \)
(b) Bestimmen Sie die darstellende Matrix von \( M_{B}^{\mathcal{B}}(f) \) von \( f \) bez. \( \mathcal{B} \).
Hallo.
Ich bräuchte hilfe bei der (b).
Für M b nach e habe ich = $$\begin{pmatrix} 1\quad0\quad1\\0\quad1\quad0\\0\quad1\quad1 \end{pmatrix}$$
Und für M e nach b habe ich = $$\begin{pmatrix} 1\quad1\quad-1\\0\quad1\quad0\\0\quad-1\quad1 \end{pmatrix}$$
Was ist der Ansatztz bei der (b)?
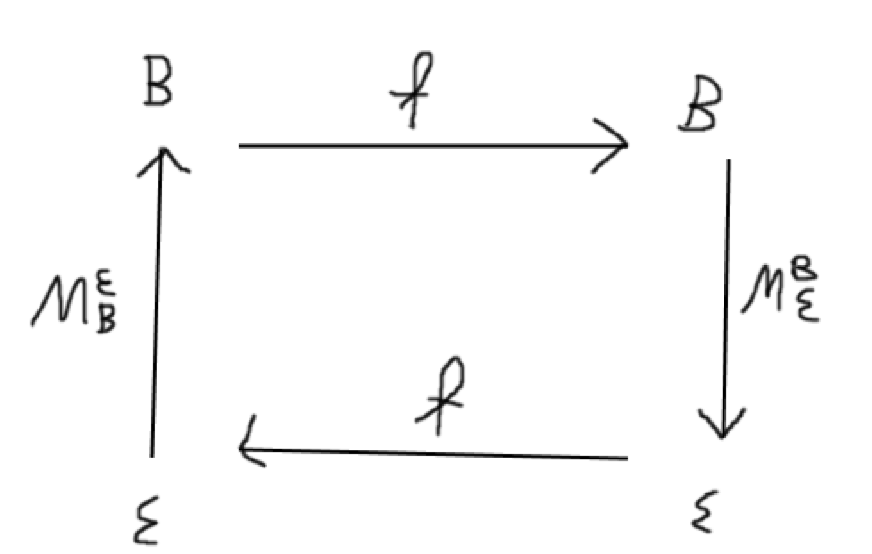
Meine Zeichnung schaut so aus: