berechnen sie den Schnittpunkt der Graphen f und g.

Question

Aufgabe: berechnen sie den Schnittpunkt der Graphen f und g. Welche Steigung hat die Gerade, die diese beiden Schnittpunkte verbindet?

F(x) = 2x^2 - 1,2x -4,4

G(x) = -0,75x^2+1,55+1,21

Comments

Hallo Lola,

wenn Du nur die Steigung \(m\) der Geraden berechnen sollst, so ist die Berechnung der Schnittpunkte nicht nötig. Die Gerade ist eine gemeinsame Sekante beider Parabeln. Und die Steigung der Parabel ist in der Mitte zwischen den beiden Schnittpunkten bei \(x=x_m\) identisch mit der Steigung der Sekante. Folglich reicht es aus, das \(x_m\) zu suchen, bei der die Parabeln die gleiche Steigung haben:$$F'(x)= 4x -1,2 \\ G'(x) = -1,5x+1,55 \\ \begin{aligned} 4x_m -1,2 &= -1,5x_m+1,55 \\ 5,5x_m &= 2,75 \\ x_m&= 0,5 \\ \implies m &= F'(x_m=0,5)= 0,8 \end{aligned}$$Das setzt natürlich voraus, dass Ihr Ableitungen von Funktionen bereits durchgenommen habt.

Und der Graph, der das ganze veranschaulichen soll:

Answer 1

Löse die Gleichung

 2x^2 - 1,2x -4,4= -0,75x^2+1,55x+1,21.

Comments

Muss man das nach dem lösen mit der PQ Formel rechnen?

---

Na, es ist eine quadratische Gleichung.

Bringe alles von rechts auf die linke Seite, damit die Gleichung die Form

2,75x² ......=0 hat und teile durch 2,75.

Erst dann kannst du die pq-Formel verwenden.

---

Ok danke! G(x) war -0,75x^2+1,55+12,1

Habe es mit der PQ Formel ausgerechnet.

Da kommt x1=3 und x2= -2 raus.

Kann das stimmen?

---

Kann das stimmen?

Was fragst du?

Berechne f(3) und g(3). Sind sie gleich?

Berechne f(-2) und g(-2). Sind sie gleich?

Nachtrag:

G(x) war -0,75x2+1,55+12,1

Ich war davon ausgegangen, dass du nach 1,55 ein x vergessen hattest

---

Lola, deine Lösungen stimmen, wenn \(G(x)=-0,75x^2+1,55x+12,1\).

Jetzt musst du nur noch deine Lösungen in F(x) oder G(x) einsetzen, um die y-Koordinaten der Schnittpunkte zu bestimmen.

---

Ups, habe das x auch vergessen.

Alles klar, Dankeschön :)

Answer 2

F := 2*x^2 - 1.2*x - 4.4
G := -0.75*x^2+1.55+1.21

x1 = -1.41
und
x2 = 1.846

G = F ( -1.41 ) = 1.269
G = F ( 1.846 ) = 0.203

Schnittpunkte
( x | y )
( -1.41 | 1.269 )
( 1.846 | 0.203 )

Gerade
y = m * x + b
m = Δ y / Δ x = ( y1 - y2 ) / ( x1 - x2)
m = ( 1.269 - 0.203 ) / ( -1.41 - 1.846 )
m = - 0.327

Einsetzen
1.269 = - 0.327 * (-1.41 ) + b
b = ...

Comments

Fehlerkorrektur
Nicht
G := -0.75*x^2+1.55+1.21
sondern
G := -0.75*x^2+1.55*x+1.21

Bin gern weiter behilflich.

Answer 3

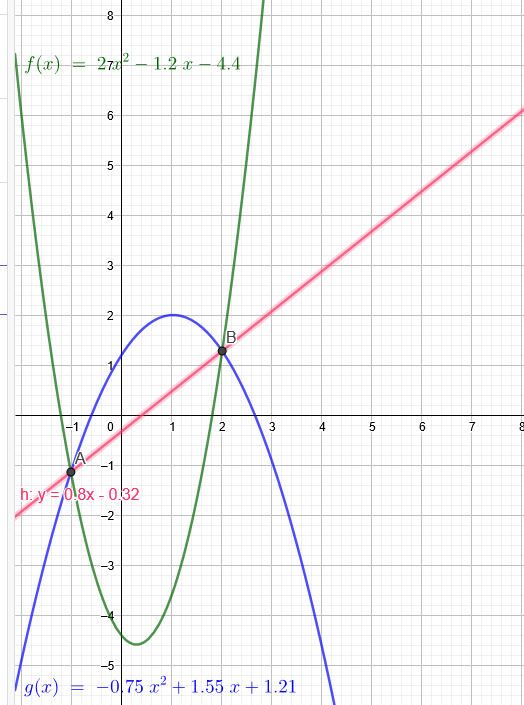
Aufgabe: berechnen sie den Schnittpunkt der Graphen f und g. Welche Steigung hat die Gerade, die diese beiden Schnittpunkte verbindet?

f(x) = 2x^2 - 1,2x -4,4
g(x) = -0,75x^2+1,55x+1,21

2x^2 - 1,2x -4,4= -0,75x^2+1,55x+1,21

2,75x^2 - 2,75x = 5,61|:2,75

x^2 - x = \( \frac{5,61}{2,75} \)=2,04

(x-0,5)^2=2,04+0,25=2,29|\( \sqrt{} \)

1.)x-0,5=\( \sqrt{2,29} \)≈1,51

x₁=2,01≈2     f(2) = 2*4 - 1,2*2 -4,4=1,2

2.)x-0,5=-\( \sqrt{2,29} \)≈-1,51

x₂=-1,01≈-1      f(-1) =  2+1,2 -4,4=-1,2

m=\( \frac{-1,2-1,2}{-1-2} \)=\( \frac{-2,4}{-3} \)=0,8