Geben Sie die Lösungsmenge folgender Ungleichung an

Question

Geben Sie die Lösungsmenge folgender Ungleichung an:
| x^2 - x - 6 | ≥ 5

Ich weiß, dass ich eine Fallunterscheidung machen muss, aber wie ist es mit dem Quadrat ?

Answer 1

Die Funktion f(x)=x^2- x - 6 hat die Nullstellen -2 und 3, und sie hat nur zwischen diesen Nullstellen negative Funktionswerte.

Damit gilt |x^2- x - 6|= x^2- x - 6, wenn x≥3 oder x≤-2 gilt.

Für -2<x<3 musst du |x^2- x - 6| in -(x^2- x - 6) umschreiben.

Answer 2

Feststellen wann der Betrag positiv oder null ist
x^2 - x - 6 = 0
x < -2
und
x > 3

Für ( x < -2 ) oder ( x > 3 ) gilt
x^2 - x - 6 ≥ 5

( x < -2.85 ) oder ( x > 3.85 )

Zusammen
( x < -2.85 ) oder ( x > 3.85 )

Der Graph der Funktion

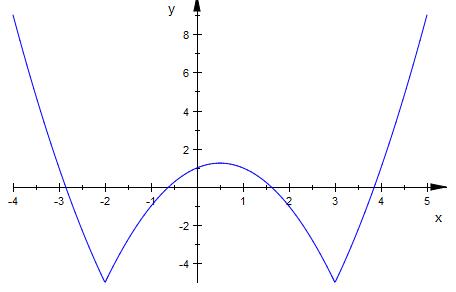
Jetzt mußt du noch den 2.Fall untersuchen.

Comments

Die schlechten Näherungswerte sind zu ersetzen durch \( \frac{1}{2} - \sqrt{\frac{45}{4}}\) und \( \frac{1}{2} + \sqrt{\frac{45}{4}}\)

Die Relationszeichen < und > sind zu ersetzen durch ≤ bzw. ≥.

---

2.Fall
Für ( x > -2 ) oder ( x < 3 ) gilt
( x^2 - x - 6 ) * -1 ≥ 5

( x > -0.62 ) oder ( x < 1.62 )

Zusammen
- 0.62 < x < 1.62

---

( x > -0.62 ) oder ( x < 1.62 )

Gilt das nicht für alle x ∈ ℝ ?

---

Für ( x > -2 ) oder ( x < 3 ) gilt

Das ist falsch, statt "oder" muss hier "und" stehen.

( x² - x - 6 ) * -1 ≥ 5

Ja, das wird hier gefordert.

( x > -0.62 ) oder ( x < 1.62 )

Das ist wieder falsch.

Kein einziges x zwischen -2 und 3 erfüllt die Ungleichung ( x² - x - 6 ) * -1 ≥ 5.

---

Hallo Arsinoë4 ,

der Graph zeigt die von mir angegeben
Lösungsmengen
( x < -2.85 ) oder ( x > 3.85 )
und
- 0.62 < x < 1.62

Für x = -2 gilt
| (-2)^2 - (-2) - 6 | ≥ 5
| 4 + 2 - 6  | ≥ 5
0 ≥ 5

x = -2 ist also nicht in der Lösungsmenge.

---

x = -2 ist also nicht in der Lösungsmenge

Immer noch: Auch dein gesamtes Intervall

- 0.62 < x < 1.62

gehört nicht zur Lösungsmenge.