kann diese aber ab dem Punkt, an dem das Gleichungssystem aufgestellt wird, nicht mehr nachvollziehen.
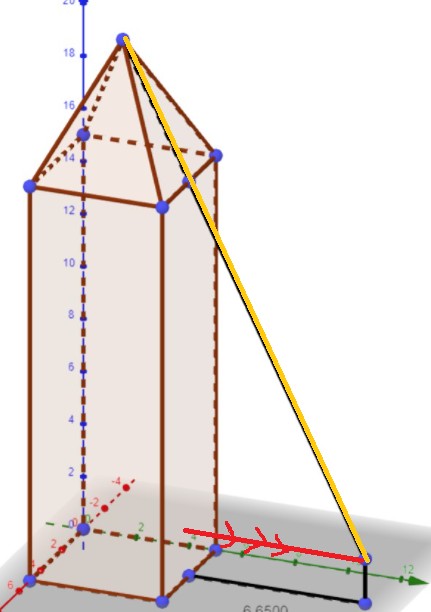
Die Kamera bewegt sich entlang der roten Geraden in einer Höhe von 1,7 Einheiten vom Turm weg.
Die Gleichung dieser Gerade ist
\( \vec{x}=\begin{pmatrix}2,5\\5\\1,7 \end{pmatrix} +s\begin{pmatrix}0\\1\\0 \end{pmatrix}\).
Die Kamera muss nur so weit bewegt werden, bis sie auf die orange eingezeichnete Gerade
\( \vec{x}=\begin{pmatrix}2,5\\2,5\\20 \end{pmatrix} +t\begin{pmatrix}0\\2,5\\-5 \end{pmatrix}\) trifft.
Der Schnittpunkt beider Geraden erfüllt mit seinen Koordinaten beide Gleichungen.
x-Koordinate: 2,5+0s = 2,5 + 0t
y-Koordinate: 5+s = 2,5 + 2,5t
z-Koordinate: 1,7 + 0s = 20-5t.
Aus der letzten Gleichung kannst du t ausrechnen und damit in der zweite Gleichung s bestimmen. (Die erste Gleichung gilt immer.)
Setzt du nun das erhaltene t=3,66 in die Gleichung der orangen Geraden ein, erhältst du einen Punkt S. Setzt du s = 6,55 in die rote Gerade ein, bekommst du den gleichen Punkt S aus der Lösung.
Der Fotograf muss also die rot eingezeichnete Strecke von der Wand bis zu diesem Punkt S zurücklegen.
Da er den Weg in dem Punkt der Geraden \(\vec{x}=\begin{pmatrix}2,5\\5\\1,7 \end{pmatrix} +s\begin{pmatrix}0\\1\\0 \end{pmatrix}\) mit dem Parameterwert 0 beginnt und in dem Punkt mit dem Parameterwert 3,66 beendet, legt er eine Strecke zuück, die 3,66 mal so lang ist wie der Betrag des dabei verwendeten Richtungsvektors.