Betragsgleichung lösen

Question

Aufgabe:

Betragsgleichung lösen

I  2x^2-4x-3  I  = 3

Problem/Ansatz:

wie löse ich diese Gleichung?

Comments

Es geht um das:

Answer 1

Mache eine Fallunterscheidung

|2·x^2 - 4·x - 3| = 3

Fall 1: 2·x^2 - 4·x - 3 ≥ 0

Fall 2: 2·x^2 - 4·x - 3 < 0

Schaffst du das dann?

Zur Kontrolle komme ich auf die Lösungen x = -1 ∨ x = 0 ∨ x = 2 ∨ x = 3

Comments

Die Fallunterscheidung konnte ich auch aufstellen, weiter weiß ich aber leider nicht.

---

Im 1. Fall können die Betragsstriche einfach weggelassen werden

Fall 1: 2·x^2 - 4·x - 3 ≥ 0

2·x^2 - 4·x - 3 = 3 --> x = 3 ∨ x = -1

Im 2. Fall lässt man die Betragsstriche weg und negiert den Entsprechenden Term

Fall 2: 2·x^2 - 4·x - 3 < 0

- (2·x^2 - 4·x - 3) = 3 --> x = 2 ∨ x = 0

Prüfe entweder, ob die entsprechenden Lösungen in den Definitionsbereich der Fallunterscheidung fallen oder prüfe generell die Lösungen auf Ihre Gültigkeit durch Einsetzen.

---

okay danke aber durch welche Rechnung kommt man denn überhaupt auf die 4 Lösungen?

---

Die Ansätze habe ich doch notiert. Kannst du nicht die enstehenden quadratischen Gleichungen lösen?

---

habe die pq-Formel angewendet komme aber auf andere, nicht so glatte ergebnisse

---

habe den fehler gefunden, danke nochmal

---

Nimm z.B. die App Photomath zur Hilfe und Selbstkontrolle.

Answer 2

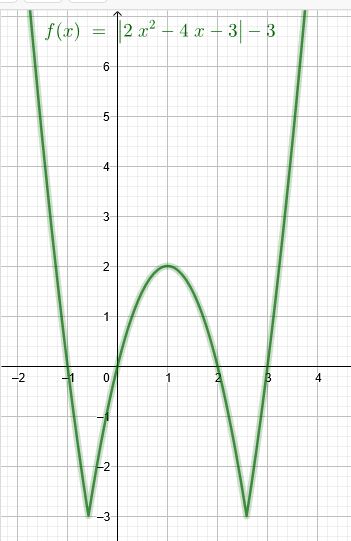
Weg ohne Fallunterscheidung:

\(|2 x^{2}  - 4 x-3| = 3|^2\)

\((2 x^{2}  - 4 x-3)^2 =3^2\)

\((2 x^{2}  - 4 x-3)^2 - 3^2=0\)

3.Binom:

\([(2 x^{2}  - 4 x-3) + 3]*[(2 x^{2}  - 4 x-3)-3]=0\)

\([2 x^{2}  - 4 x]*[2 x^{2}  - 4 x-6]=0\)

1.) \([2 x^{2}  - 4 x]=0\)\)   →     \([ x^{2}  - 2 x]=0\)     \( x₁=0\)       \( x₂=2\)

2.) \([2 x^{2}  - 4 x-6]=0\)  

→  \( x^{2}  - 2 x=3\)  →  \( (x - 1)^2=3+1=4\)

\( x - 1=2\)     \( x₃=3\)

\( x - 1=-2\)     \( x₄=-1\)

Probe für   \( x₁=0\)     \(|-3|=3\)✓

Probe für \( x₂=2\)      \( |2 *2^{2} - 4*2-3| = 3\) ✓

Probe für \( x₃=3\)       \(|2 *3^{2}  - 4 *3-3| = 3\)✓

Probe für \( x₄=-1\)      \(|2 *(-1)^{2}  - 4 *(-1)-3| = 3\)✓