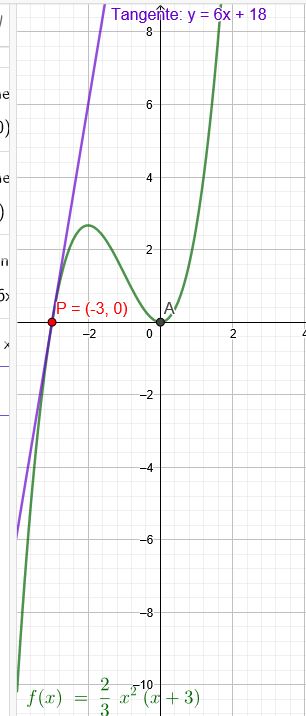
Bestimme eine Gleichung einer ganzrationalen Funktion 3.

Question

Aufgabe: Bestimme eine Gleichung einer ganzrationalen Funktion 3. Grades, deren Graph die x-Achse im Ursprung berührt und deren Tangente in P(-3|0) parallel zu y=6x ist.

Problem: Ich weiß nicht, wie ich das machen soll. Bitte helft mir !

Answer 1

f(x) = ax³+bx²+cx+d

f(0)= 0

f '(0) = 0

f(-3) = ß

f '(-3) = 6

Stelle das Gleichungssystem auf!

Answer 2

" Bestimme eine Gleichung einer ganzrationalen Funktion 3. Grades, deren Graph die x-Achse im Ursprung berührt und deren Tangente in $P(-3|0)$ parallel zu $y=6x$ ist."

deren Graph die x-Achse im Ursprung berührt  und   $P(-3|0)$ liegt auf dem Graphen:

$f(x)=a*x^2*[x-(-3)]=a*x^2*(x+3)=a*x^3+3*a*x^2$

Tangentensteigung in $P(-3|0)=6$ :

$f´(x)=3*a*x^2+6*a*x$

$f´(-3)=3*a*(-3)^2+6*a*(-3)=27a-18a=9a=6$        →  $a=\frac{6}{9}=\frac{2}{3}$

$f(x)=\frac{2}{3}*x^2*(x+3)$