Du kannst auf der Koordinatenform der Ebene ja ganz leicht die Spurpunkte der Ebene ausrechnen.
Du weißt was die Spurpunkte sind und wie man sie berechnet?
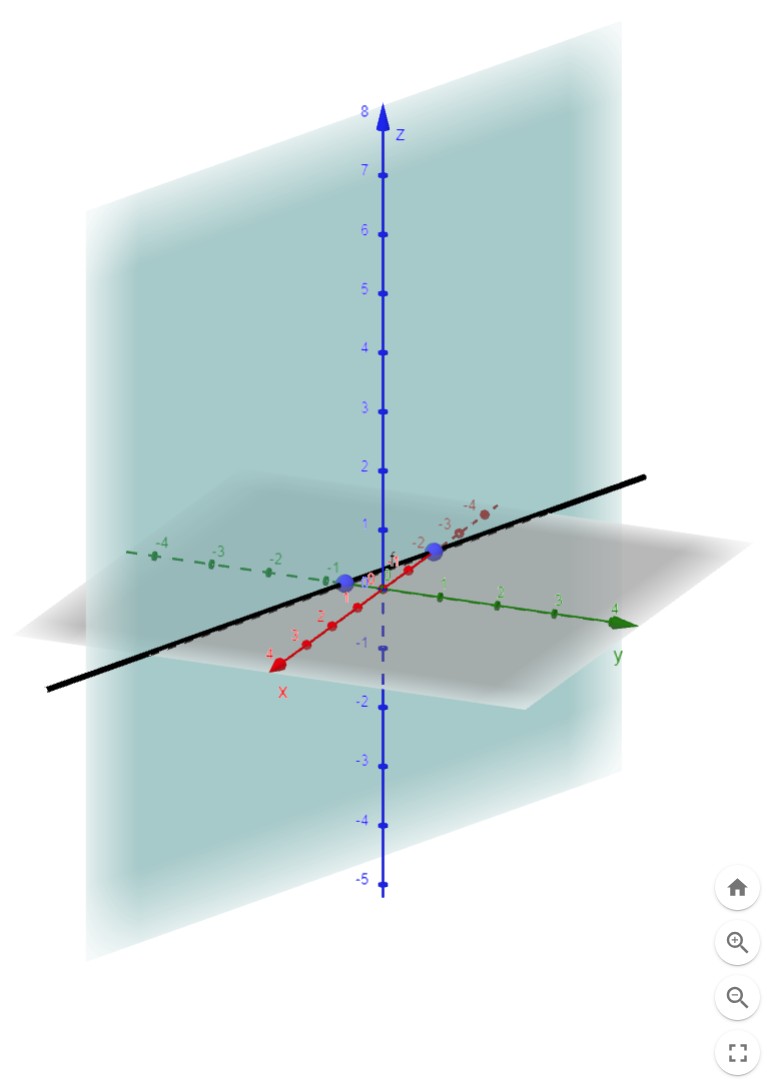
Spurpunkte sind (-2, 0, 0) und (0, -2/3, 0). Auf der z-Achse gibt es keinen Spurpunkt. Das bedeutet die z-Achse wird nicht von der Ebene geschnitten. Also verläuft die Ebene parallel zur z-Achse.
Hier eine Skizze mit Spurgerade und Spurpunkten.