Figur mit Parallelen und Kreisbogen. Wie ermittelt ich den fehlenden Winkel?

Question

Aufgabe:Die Geraden AB und DC liegen parallel zueinander. Ermitteln Sie die Größe des Winkels ε.

Problem/Ansatz:

Kann ich dann von ausgehen, dass der Kreisbogen um D geschlagen wurde und somit das Dreieck DBC ein gleichschenkliges Dreieck ist, sowie das Dreieck ABD?

Liebe Grüße und Dank

Answer 1

die Winkel im Punkt $D$ sind der Schlüssel zur Lösung.

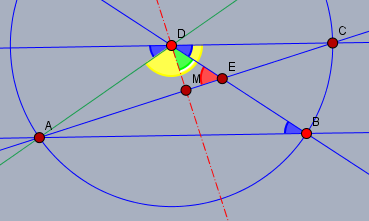
Die blauen Winkel sind alle gleich groß ($34°$). Daraus folgt dann der Winkel $\angle ADC$ (gelb). Die rote Strich-Punkt-Gerade durch $DM$ halbiert das Dreieck $\triangle ACD$ und damit auch den Winkel $\angle ADC$. Zieht man von der Hälfte den Winkel $\angle BDC$ (blau) ab, so erhält man den Winkel $\angle MDE$ (grün). Das Dreieck $\triangle MED$ ist ein rechtwinkliges. $$\implies \epsilon = \angle DEA = 51°$$

"Mathematik ist ein wundersames Spiel mit überraschenden Zusammenhängen, eine Kunstform, die man ausfüllen kann wie Musik. Da steckt so viel Spannendes drin, das Mysterium der Primzahlen, die Magie der Endlos-Zahl Pi. Oder Geometrie, da kann ich weinen vor Begeisterung." Ranga Yogeshwar (aus Süddeutsche Zeitung vom 11.Juni 2019)

Comments

∠BDC = 34° (Wechselwinkel an ||)
∠BAC = 34°/2 = 17° (Zentrums-Peripherie-Winkel-Satz)
ε = 17° + 34° = 51° (Außenwinkelsatz)

---

Danke, auf die Lösung bin ich gekommen. War mir halt unsicher, ob ich davon ausgehen kann, dass der Kreis um D gezogen wurde.

Vielen Dank

Answer 2

Hallo

 ja davon kannst du ausgehen, sonst ist das nicht lösbar,  also DC=DA=DC

Gruß lul