Wie berechne ich eine Seite oder einen Winkel im Dreieck DCE?

Question

Aufgabe:

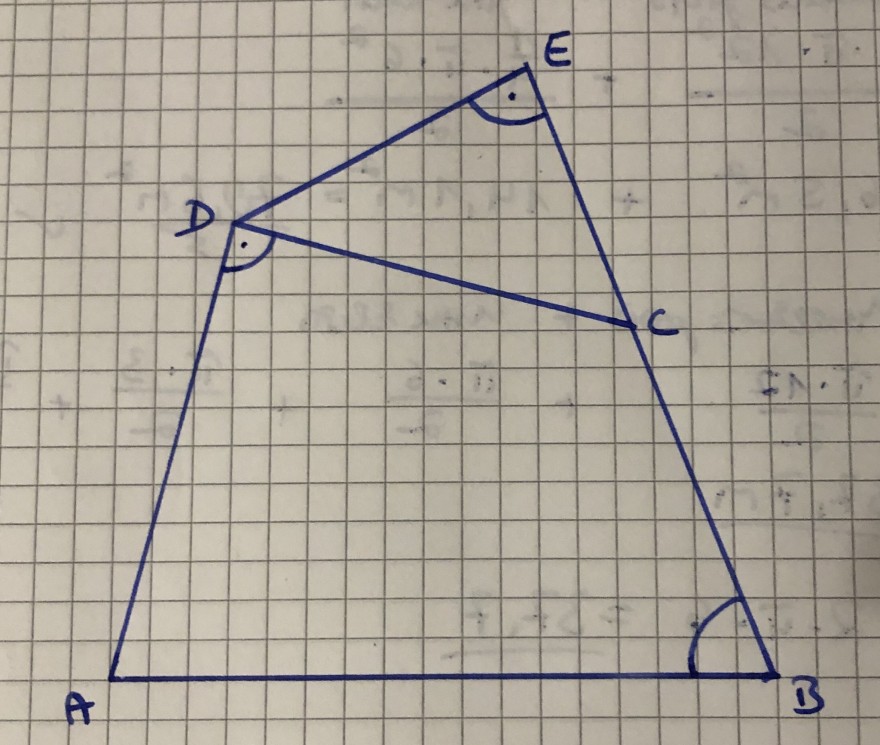
Ein Baumarkt plant die Erweiterung des Außengeländes. Berechnen Sie die Länge der Strecke AC sowie den Flächeninhalt des Außengeländes nach der Erweiterung.

Viereck ABCD ist das Baumarktgelände und Dreieck CDE ist die Erweiterung

gegeben: AB=410m, AD=260m, BC=240m, Winkel CBA= 56,3 Grad

Problem/Ansatz:

Ich habe schon Strecke AC berechnet (= 341,3m) und auch den Winkel ACD (49,6 Grad) und Winkel CAD (40,4 Grad) im Dreieck ACD. Weiterhin habe ich auch schon die Strecke CD (221,2m). Jedoch weiß ich nicht wie ich weiter machen soll, um auf einen Winkel oder eine Seite im Dreieck DCE zu kommen.

Comments

Die beiden Winkel bei C ergänzen sich zu 180°, wenn man also den im unteren Viereck berechnen kann, dann auch den anderen.

Answer 1

Die Seite AC bekommst du mit dem cos-Satz im Dreieck ABC , ich bekomme AC=341,3m

Dann Pythagoras in ACD gibt für CD = 221,1m.

Den Innenwinkel bei C im Dreieck ABC mit Sem sin-Satz

sin (γ) / 410 = sin(56,3°) / 341,3  ==>    γ ≈ 90° .

Rest ist dann einfach.